Cho hs \(y=x^4-\left(3m-1\right)x^2+2m+1\).Tìm m để đồ thị hàm số có 3 điểm cực trị A, B, C cùng với điểm D(7;3) nội tiếp được một đường tròn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
23 tháng 4 2016
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
a. Hàm có 3 cực trị \(\Rightarrow m< 0\)
\(y'=8x^3+4mx=4x\left(2x^2+m\right)=0\Rightarrow\left[{}\begin{matrix}x=0;y=-\dfrac{3m}{2}\\x=-\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\\x=\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\end{matrix}\right.\)
Trong đó \(A\left(0;-\dfrac{3m}{2}\right)\) là cực đại và B, C là 2 cực tiêu
Do tam giác ABC luôn cân tại A \(\Rightarrow\) tâm I của đường tròn ngoại tiếp luôn nằm trên trung trực BC hay luôn nằm trên Oy
Mà tứ giác ABCO nội tiếp \(\Rightarrow OI=AI\Rightarrow I\) là trung điểm OA (do I, O, A thẳng hàng, cùng nằm trên Oy)
\(\Rightarrow I\left(0;-\dfrac{3m}{4}\right)\)
Mặt khác trung điểm BC cũng thuộc Oy và IB=IC (do I là tâm đường tròn ngoại tiếp)
\(\Rightarrow\) I trùng trung điểm BC
\(\Rightarrow-\dfrac{3m}{4}=-\dfrac{m^2+3m}{2}\) \(\Rightarrow m\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
b.
Từ câu a ta thấy khoảng cách giữa 2 cực đại là:
\(\left|x_B-x_C\right|=2\sqrt{-\dfrac{m}{2}}=5\Rightarrow m=-\dfrac{25}{2}\)
23 tháng 4 2016
Hàm số đã cho có 3 điểm cực trị \(\Leftrightarrow y'=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3-2\left(3m+1\right)x=0\) có 3 nghiệm phân biệt \(\Leftrightarrow m>-\frac{1}{3}\) (1)
Khi đó 3 điểm cực trị của đồ thị là \(A\left(0;2m+2\right);B\left(-\sqrt{6m+2};-9m^2-4m+1\right);C\left(\sqrt{6m+2};-9m^2-4m+1\right)\)
Rõ ràng tam giác ABC cân tại A và trung tuyến kẻ từ A thuộc Oy. Do đó O là trọng tâm của tam giác ABC \(\Leftrightarrow y_A+2y_B=0\)
Hay \(2m+2+2\left(-9m^2-4m+1\right)=0\Leftrightarrow9m^2+3m-2=0\)
Suy ra \(m=-\frac{2}{3}\) hoặc \(m=\frac{1}{3}\)
Kết hợp với (1) suy ra giá trị của m là \(m=\frac{1}{3}\)
CM
24 tháng 8 2017
Chọn A
[Phương pháp trắc nghiệm]
Hàm số có 3 điểm cực trị khi m > 1 3
Áp dụng công thức:
Phương trình đường tròn ngoại tiếp ∆ A B C là:
Thay vào ta có phương trình:
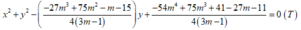
Sử dụng chức năng SOLVE ,
tìm ra nghiệm duy nhất thỏa mãn là m = 3
ta tính \(y'=4x^3-2\left(3m-1\right)x=2x\left(2x^2-3x+1\right)\)
để hàm số có 3 cực trị thì pt y'=0 có 3 nghiệm phân biệt
ta có
\(y'=0\Leftrightarrow2x\left(2x^2-3m+1\right)=0\Rightarrow x=0;2x^2=3m-1\)
để pt có 3 nghiệm phân biệt thì 3m-1>0 suy ra m>1/3
x=0 ta có y=2m+1 suy ra \(A\left(0;2m+1\right)\) ;\(B\left(\sqrt{\frac{3m-1}{2}};-\frac{\left(3m-1\right)^2}{4}+2m+1\right)\); \(C\left(-\sqrt{\frac{3m-1}{2}};\frac{-\left(3m-1\right)^2}{4}+2m+1\right)\)
ta có \(\vec{AB}\left(\sqrt{\frac{3m-1}{2}};\frac{-\left(3m-1\right)^2}{4}\right)\); \(\vec{AC}=\left(-\sqrt{\frac{3m-1}{2}};-\frac{\left(3m-1\right)^2}{4}\right)\)
suy ra AC=AB suy ra tam giác ABC cân tại A
Gỉa sử A,B,C,D nội tiếp đường tròn suy ra tâm của đường tròn nằm trên trung tuyến BC
do tam giác ABC cân tại A suy ra trung tuyến BC cũng chính là đường cao của BC
ta có
\(\vec{BC}=\left(2\sqrt{\frac{3m-1}{2}};0\right)\)
phương trình đường cao qua A và vuông góc với BC nhận \(\vec{BC}\)làm vecto pháp tuyến có dạng
\(2\sqrt{\frac{3m-1}{2}}\left(x-0\right)+0\left(y-2m-1\right)=0\Rightarrow x=0\)(d)
Gọi I(0;a) thuộc (d) là tâm đường tròn mà A,B,C,D nội tiếp
suy ra ta có hệ pt
\(\begin{cases}IA=IB\\IB=IC\\IC=ID\end{cases}\)
giải ra ta tim đc mKết quả là j ạ