trên mặt nước có 2 nguồn A, B dao động lần lượt theo phương trình
Ua=acos(wt) cm
Ub=acos(wt+pi/3) cm
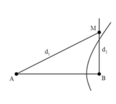
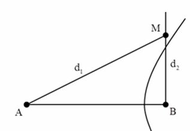
với bước sóng lamđa = 3cm. Điểm M trên phương truyền sóng dao động với biên độ cực đại.
biết M cách nguồn A,B lần lượt là d1 và d2. cặp giá trị có thể của d1 và d2 là?
đáp án: d1=12cm d2=18,5cm

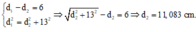
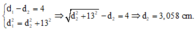



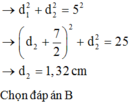
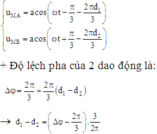
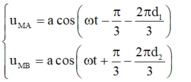
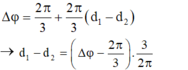
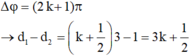
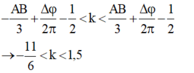
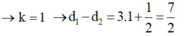
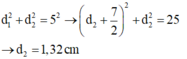
Mình giải thích chi tiết hơn công thức của bạn Giang Nam thế này:
B sớm pha hơn A là \(\frac{\pi}{3}\)
Mình lấy điểm B' trên phương truyền sóng BM sao cho B' cùng pha với A, nên B' trễ pha \(\frac{\pi}{3}\)so với B \(\Rightarrow BB'=\frac{\lambda}{6}\)
B' cùng pha với A nên B dao động cực đại thì: \(MB'-MA=k\lambda\Leftrightarrow\left(d_2-\frac{\lambda}{6}\right)-d_1=k\lambda\)
\(\Leftrightarrow d_2-d_1=k\lambda+\frac{\lambda}{6}\)(Trong công thức của bạn Giang Nam phải sửa lại như thế này mới đúng đc)
Dựa theo các phương án của bài toán thì d1=12cm, d2 = 18cm thỏa mãn công thức trên nên điểm M dao động biên cực đại.
Điểm M dao động với biên cực đại khi: \(d_2-\left(d_1-\frac{\lambda}{6}\right)=k\lambda\Rightarrow d_2-d_1=k\lambda-\frac{\lambda}{6}\)
Thử giá trị: \(d_2-d_1=6,5=2\lambda-\frac{\lambda}{6}\) thỏa mãn điều kiện cực đại ở trên nên điểm M dao động với biên cực đại.