Câu 13
Từ các số hạng đã biết 2D, 1G, 6S hãy xác định các trạng thái ứng với mức năng lượng có thể có trong phân tử.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Theo tiên đề Bo thứ II ta có:
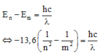
+ Áp dụng cho quá trình từ n = 5 về n = 4 ta có:
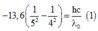
+ Áp dụng cho quá trình từ n = 4 về n = 2 ta có:
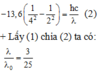
=> Chọn B.

Chọn đáp án B
Theo tiên đề Bo thứ II ta có: E n − E m = h c λ ⇔ − 13 , 6 1 n 2 − 1 m 2 = h c λ
Áp dụng cho quá trình từ n = 5 về n = 4 ta có: − 13 , 6 1 5 2 − 1 4 2 = h c λ 0 ( 1 )
Áp dụng cho quá trình từ n = 4 về n = 2 ta có: − 13 , 6 1 4 2 − 1 2 2 = h c λ ( 2 )
Lấy (1) chia (2) ta có: λ λ 0 = 3 25
Ta có: Kí hiệu thể hiện trạng thái nguyên tử có dạng \(^{2S+1}X_J\) trong đó
- S; là giá trhij momen động lượng spin tổng
- 2S+1: là độ bội; J: là giá trị momen toàn phần chủa toàn nguyên tử;
- X là kí hiệu tương ứng với giá trị của momen động lượng L
Vậy
a)Đối với số hang: \(^2D\) ta có độ bội 2S+1=2 suy ra S= 1/2 và kí hiệu D tương ứng với L=2
J= |L-S| = |2-\(\frac{1}{2}\)|= \(\frac{3}{2}\) hoặc J = |L+S| = |2+\(\frac{1}{2}\)| =\(\frac{5}{2}\)
vậy từ số hạng đã biết là \(^2D\) ta có trạng thái ứng với mức năng lượng có thể có trong phân tử là \(^2D_{\frac{3}{2}}\) và \(^2D_{\frac{5}{2}}\).
b) Đối với số hạng: \(^1G\) tương tự ta có độ bội 2S+1=1 nên S=0 và kí hiệu G tương ứng L=4
J=|L-S| = |4-0| =4 hoặc J= |L+S| = |4+0|= 4
Vậy ta có trạng thái ứng với mức năng lượng của số hạng có thể có trong phân tử là : \(^1G_4\).
c) Đối với số hạng: \(^6S\) tương tự ta có độ bội là 2S+1=6 nên S= \(\frac{5}{2}\) và kí hiệu S ứng với L=0
J=|L+S|= |0+\(\frac{5}{2}\)| = \(\frac{5}{2}\) hoặc J= |L-S|=|0-\(\frac{5}{2}\)|=\(\frac{5}{2}\)
vậy ta có trạng thái ứng với mức năng lượng của số hạng đã biết có thể có trong phân tử là : \(^6S_{\frac{5}{2}}\)
Số hạng nguyên tử có dạng : 2S+1XJ
*/số hạng 2D \(\Rightarrow\) 2S + 1 = 2 \(\Rightarrow\)đội bội : S = \(\frac{1}{2}\) ; mặt khác S = \(\frac{N}{2}\) \(\Rightarrow\)N = 1 vậy số e độc thân = 1
số hạng ứng với X = D \(\Rightarrow\)L = 2 ; J = | L+ S | \(\Rightarrow\)J = |2+ \(\frac{1}{2}\)| = \(\frac{5}{2}\) và J = | 2 - \(\frac{1}{2}\)| = \(\frac{3}{2}\)
nên số hạng 2D ứng với trạng thái 2D\(\frac{3}{2}\) và 2D\(\frac{5}{2}\)
*/số hạng 1G \(\Rightarrow\) 2S + 1 = 1 \(\Rightarrow\)đội bội : S = 0 ; mặt khác S = \(\frac{N}{2}\) \(\Rightarrow\)N = 0 vậy số e độc thân = 0
số hạng ứng với X = G \(\Rightarrow\)L = 4 ; J = | L+ S | \(\Rightarrow\)J = |4+ 0| = 4 và J = | 4 - 0| = 4
nên số hạng 2G ứng với trạng thái 2G4
*/số hạng 6S \(\Rightarrow\) 2S + 1 = 6 \(\Rightarrow\)đội bội : S = \(\frac{5}{2}\) ; mặt khác S = \(\frac{N}{2}\) \(\Rightarrow\)N = 5 vậy số e độc thân = 5
số hạng ứng với X = S \(\Rightarrow\)L = 0 ; J = | L+ S | \(\Rightarrow\)J = | 0+\(\frac{5}{2}\)| =\(\frac{5}{2}\) và J = | 0-\(\frac{5}{2}\)| = \(\frac{5}{2}\)
nên số hạng 6S ứng với trạng thái 6S\(\frac{5}{2}\)