Tìm giá trị lớn nhất hoặc nhỏ nhất của đa thức
K
Khách
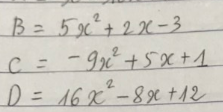
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
ND
1
21 tháng 10 2016
A=...
dăt 5x=y viet cho gon
x=y/5
-A=y^2-y/5+3
=(y-1/10)^2+3-1/100
A=-(y-1/10)^2-299/100
GTLN=-299/100 khi y=1/10
BK
1
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Lời giải:
Ta có:
$x^2-3x+11=(x-\frac{3}{2})^2+\frac{35}{4}\geq \frac{35]{4}$
$\Rightarrow \frac{31}{x^2-3x+11}\leq 31:\frac{35}{4}=\frac{124}{35}$
$\Rightarrow \frac{31}{x^2-3x+11}+15\leq \frac{649}{35}$
Vậy gtln của biểu thức là $\frac{649}{35}$ khi $x=\frac{3}{2}$
ND
1
CW
20 tháng 10 2016
\(-5x^2+x-7=-5\left(x^2-\frac{1}{5}x+\frac{7}{5}\right)=-5\left(x^2-2\cdot\frac{1}{10}\cdot x+\frac{1}{100}-\frac{1}{100}+\frac{7}{5}\right)\)
\(=-5\left(x-\frac{1}{10}\right)^2+\frac{139}{20}\)
\(-5\left(x-\frac{1}{10}\right)^2+\frac{139}{20}\le\frac{139}{20}\)
GTLN của đa thức trên là 139/20
BK
0
AP
2
MT
28 tháng 5 2015
B=2x2+10x-1
=2(x2+5x-\(\frac{1}{2}\))
=2(x2+2x.\(\frac{5}{2}\)\(+\frac{25}{4}\)\(-\frac{27}{4}\))
=2[(x2+\(\frac{5}{2}\))2-\(\frac{27}{4}\)]
=2(x+\(\frac{5}{2}\))2-\(\frac{27}{2}\)\(\ge\frac{-27}{2}\)(vì (x+5/2)2\(\ge0\))
Dấu = xảy ra khi :
x+\(\frac{5}{2}\)=0
<=>x=\(\frac{-5}{2}\)
Vậy GTNN của B là \(\frac{-27}{2}\)khi x= \(\frac{-5}{2}\)
NP
0
ND
2
20 tháng 10 2016
A = 2x^2 +10x - 1
2A = 4x^2 + 20x -1
2A = (2x+5)2 - 26
A = (2x+5)2/2 - 13
A có GTNN thì (2x+5)2/2 = 0
2x+ 5 =0
x = -5/2
16 tháng 8 2021
b: Ta có: \(x^2-x+5\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{19}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\forall x\)
\(\Leftrightarrow\dfrac{2022}{\left(x-\dfrac{1}{2}\right)^2+\dfrac{19}{4}}\le\dfrac{8088}{19}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$
$=5(x+\frac{1}{5})^2-\frac{16}{5}$
$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$
---------------------------------
$C=-9x^2+5x+1=1-(9x^2-5x)$
$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$
$=\frac{61}{36}-(3x-\frac{5}{6})^2$
$\leq \frac{61}{36}$
Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$
-----------------------
$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$
$=(4x-1)^2+11\geq 0+11=11$
Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$