1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB < HA). Vẽ dây CD vuông góc với AB...
Đọc tiếp
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn
2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB < HA). Vẽ dây CD vuông góc với AB tại H. CMR:
a) Góc BCA = 90 độ b) CH . HD = HB . HA c) Biết OH = R/2. Tính diện tích tam giác ACD theo R
3/ Cho tam giác MAB, vẽ đường tròn (O) đường kính AB cắt MA ở C, cắt MB ở D. Kẻ AP vuông góc CD , BQ cuông góc CD. Gọi H là giao điểm AD và BC. CM:
a) CP = DQ b) PD . DQ = PA . BQ và QC . CP = PD . QD c) MH vuông góc AB\
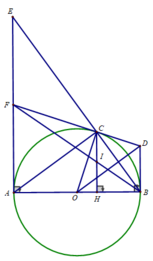
4/ Cho đường tròn (O;5cm) đường kính AB, gọi E là 1 điểm trên AB sao cho BE = 2cm.Qua trung điểm kH của đoạn AE vẽ dây cung CD vuông góc AB.
a) Tứ giác ACED là hình gì? Vì sao? b)Gọi I là giao điểm của DE với BC. CMR:I thuộc đường tròn (O') đường kính EB
c) CM HI là tiếp điểm của đường tròn (O') d) Tính độ dài đoạn HI
5/ Cho đường tròn (0) đường kính AB = 2R. Gọi I là trung điểm của AO, qua I kẻ dây CD vuông góc với OA.
a) Tứ giác ACOD là hình gì? tại sao?
b) CM tam giác BCD đều
c) Tính chu vi và diện tích tam giác BCD theo R
6/ Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 9cm; BC = 15cm
a) Tính độ dài các cạnh AC, AH, BH, HC
b) Vẽ đường tròn tâm B, bán kính BA. Tia AH cắt (B) tại D. CM: CD là tiếp tuyến của (B;BA)
c) Vẽ đường kính DE. CM: EA // BC
d) Qua E vẽ tiếp tuyến d với (B). Tia CA cắt d tại F, EA cắt BF tại G. CM: CF = CD + EF và tứ giác AHBG là hình chữ nhật
7/ Cho đường tròn (O) đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. gọi E là giao điểm của AC và BM.
a) CMR: NE vuông góc AB
b) Gọi F là điểm đối xứng với E qua M. CMR: FA là tiếp tuyến của đường tròn (O)
c) CM: FN là tiếp tuyến của đường tròn (B;BA)
8/ Cho nửa đường tròn (O), đường kính AB.Từ một điểm M trên nửa đường tròn ta vẽ tiếp tuyến xy. Từ A ta vẽ AD vuông góc với xy tại D
a) CM: AD // OM
b) Kẻ BC vuông góc với xy tại C. CMR: MC = MD