tìm số tự nhiên n để hai số : 7n+ 13 và 2n+4 là hai số nguyên tố cùng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
22 tháng 7 2021
Đúng(0)
Những câu hỏi liên quan
NV
0
CA
4
8 tháng 7 2018
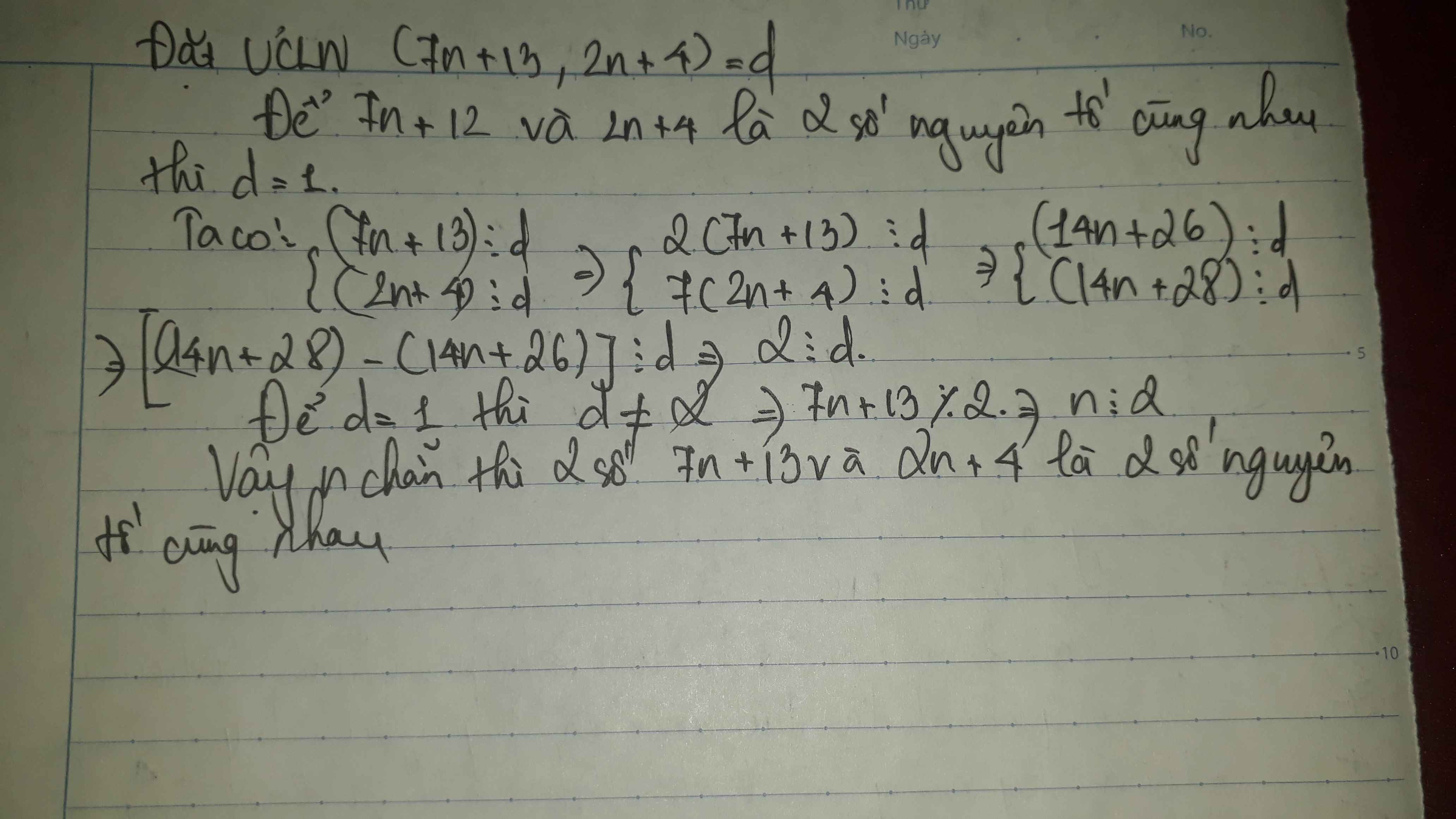
Để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
<=> ƯCLN(2n+1;7n+2) = 1
<=> 7.(2n+1)-2.(7n+2) chia hết cho 1
<=> 14n+7-14n-4 chia hết cho 1
<=> 3 chia hết cho 1
Vậy n = 3 (thỏa mãn \(n\in N\) )
8 tháng 7 2018
mik thấy câu rả lời này nhiều lắm,chắc các bn copy của nhau chớ gì.mik cần câu trả lời tự làm của các bn nhưng phải chi tiết ,rõ ràng và chính xác
HH
0
NK
7
28 tháng 7 2015
Để 2n + 1 và 7n + 2 nguyên tố cùng nhau
<=> ƯCLN(2n + 1; 7n + 2) = 1
<=> 7.(2n + 1) - 2.(7n + 2) chia hết cho 1
<=> 14n + 7 - 14n + 4 chia hết cho 1
<=> 3 chia hết cho 1
Vậy n = 3
KT
0
DB
0
28 tháng 11 2017
Ta có { 2[ 7n+13 ] ; 7[ 2n+4 } = { 14n+ 26 ; 14n + 28 } suy ra
14n + 28 - 14n+26 = 2 . Suy ra n = 2 thỏa mãn
Bài này mình làm tắt
CC
0
PT
1
CM
6 tháng 10 2019
Vì 7n+13 và 2n+4 nguyên tố cùng nhau nên ta gọi d = UCLN(7n+13,2n+4)
=>7n+13 ⋮ d và 2n+4 ⋮ d
Có 7n+13 ⋮ d => 2(7n+13) ⋮ d => 14n+26 ⋮ d
2n+4 ⋮ d => 7.(2n+14) ⋮ d => 14n+28 ⋮ d
Suy ra (14n+28) – (14n+26) ⋮ d => 2 ⋮ d => d ∈ {1;2}
Nếu d = 1 thì 7n+13 và 2n+4 là nguyên tố cùng nhau
Nếu d = 2 => 7n+13 ⋮ 2 => 7.(n+1)+6 ⋮ 2 vì 6 ⋮ 2 nên 7.(n+1) ⋮ 2 mà UC(7,2) = 1 => n+1 ⋮ 2
Để n+1 ⋮ 2 thì n = 2k+1
Vậy để 7n+13 và 2n+4 là số nguyên tố cùng nhau thì n ≠ 2k+1
