Giải giúp mình bài 1, 2 với ạ, nếu được thì giải kĩ phần tính diện tích tam giác giúp mình, mình không hiểu phần đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

coi chiều dài hình chữ nhật là 100%
chiều dài hình chữ nhật lúc sau là
100%+60%=160%(so với chiều dài cũ)
coi diện tích ban đầu là 100%
chiều rộng lúc sau là
100%:160%=62,5%(so với chiều rộng cũ)
chiều rộng giảm số % là
100%-62,5%=37,5%
đáp số:37,5 %
tick nha Princess of the Stars

Dien h mot mat la :
216 : 6 =36 (cm2)
Dien h xung quanh la :
36 x 4 =144 (cm2)
Dap so : 144 cm2.

1. Chiều cao hình thang đó là:
7/8:7/4=1/2(m)
Đáp số : 1/2m
2. Độ dài đáy hình tam giác đó là :
3/8 : 2/3=9/16(m)
Đáp số : 9/16m
3.Diện tích cánh cửa là :
2,4x0,8=1,92(m2)
Diện tích phần cửa đã sơn là:
2,4x0,8:2=0,96(m2)
Diện tích phần cửa chưa sơn là :
1,92-0,96=0.96(m2)
Đáp số : 0.96 m2

bai 1 ban tinh phan so nhu binh thuong nhe
bai 2 dau tien ban tim chieu cao bang phan duoc mo rong sau do tim day la 12 nhan 5/4 bang 15 vay buoc cuoi la
12 nhan 15 chia 2 bang 90 nhe

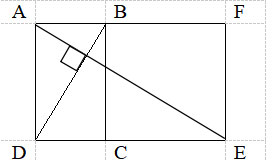
a) Gọi giao điểm của AE và BD là H
Ta có diện tích tam giác ADE bằng
Diện tích tam giác ABE bằng
Vậy diện tích tứ giác ABED bằng tổng diện tích tam giác ADE và tam giác ABE và bằng hay diện tích tứ giác ABED bằng
Vậy diện tích tứ giác ABED là:
( )
b) Tứ giác ABED cũng là một hình thang với đáy nhỏ AB, đáy lớn DE và chiều cao AD
Vì nên
Diện tích tam giác DBE gấp 3 lần diện tích tam giác DAB vì chiều cao BC bằng chiều cao DA, đáy DE gấp 3 lần đáy AB. Vậy diện tích tam giác DBE sẽ bằng diện tích hình thang ABCD
Diện tích tam giác DBE là:
( )
Diện tích tam giác BCE gấp 2 lần diện tích tam giác BCD vì hai tam giác chung chiều cao BC, đáy CE gấp 2 lần đáy CD. Vậy diện tích tam giác BCE sẽ bằng diện tích tam giác DBE
Diện tích tam giác BCE là:
( )
Diện tích tam giác BCD là:

1.
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)