Tìm số nguyên tố a sao cho a + 10 và a + 14 cũng là số nguyên tố ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
18 tháng 7 2015
b) +) Nếu p = 3k + 1 (k thuộc N)=> 2p2 + 1 = 2.(3k + 1)2 + 1 = 2.(9k2 + 6k + 1) + 1 = 18k2 + 12k + 2 + 1 = 18k2 + 12k + 3 chia hết cho 3 và lớn hơn 3 => 2p2 + 1 là hợp số (loại)
+) Nếu p = 3k + 2 (k thuộc N) => 2p2 + 1 = 2.(3k + 2)2 + 1 = 2.(9k2 + 12k + 4) + 1 = 18k2 + 24k + 8 + 1 = 18k2 + 24k + 9 chia hết cho 3 và lớn hơn 3 => 2p2 + 1 là hợp số (loại)
Vậy p = 3k, mà p là số nguyên tố => k = 1 => p = 3
18 tháng 7 2015
a) +) Nếu p = 1 => p + 1 = 2; p + 2 = 3; p + 4 = 5 là số nguyên tố
+) Nếu p > 1 :
p chẵn => p = 2k => p + 2= 2k + 2 chia hết cho 2 => p+ 2 là hợp số => loại
p lẻ => p = 2k + 1 => p + 1 = 2k + 2 chia hết cho 2 => p+1 là hợp số => loại
Vậy p = 1
c) p = 2 => p + 10 = 12 là hợp số => loại
p = 3 => p + 10 = 13; p+ 14 = 17 đều là số nguyên tố => p = 3 thỏa mãn
Nếu p > 3 , p có thể có dạng
+ p = 3k + 1 => p + 14 = 3k + 15 chia hết cho 3 => loại p = 3k + 1
+ p = 3k + 2 => p + 10 = 3k + 12 là hợp số => loại p = 3k + 2
Vậy p = 3
8 tháng 11 2014
a; nếu p=3 thì p+2=5 , p+4=7 đều là số nguyên tố
nếu p>3 thì p có 2 dạng : p=3k+1, p=3k+2
với p=3k+1 thì p+2=3k+1+2=3k+3 chia hết cho 3 => p+2 là hợp số
với p=3k+2 thì p+4=3k+2+4=3k+6 '''''''''''''''''''''''''''''''''''''''''''' =>p+4 là hợp số
Vậy p=3 thỏa mãn đề bài
các phần còn lại tương tự
1 tháng 8 2017
hinh nhu may bai nay lop tren thi phai minh hoc lop 5 ma khong biet
LV
15 tháng 11 2017
Câu đó này khó đến cả mình không giải được!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
PV
0
13 tháng 8 2021
Câu b:
Đến đoạn này cũng xét như câu a
Câu c:
HT
1
TL
17 tháng 6 2015
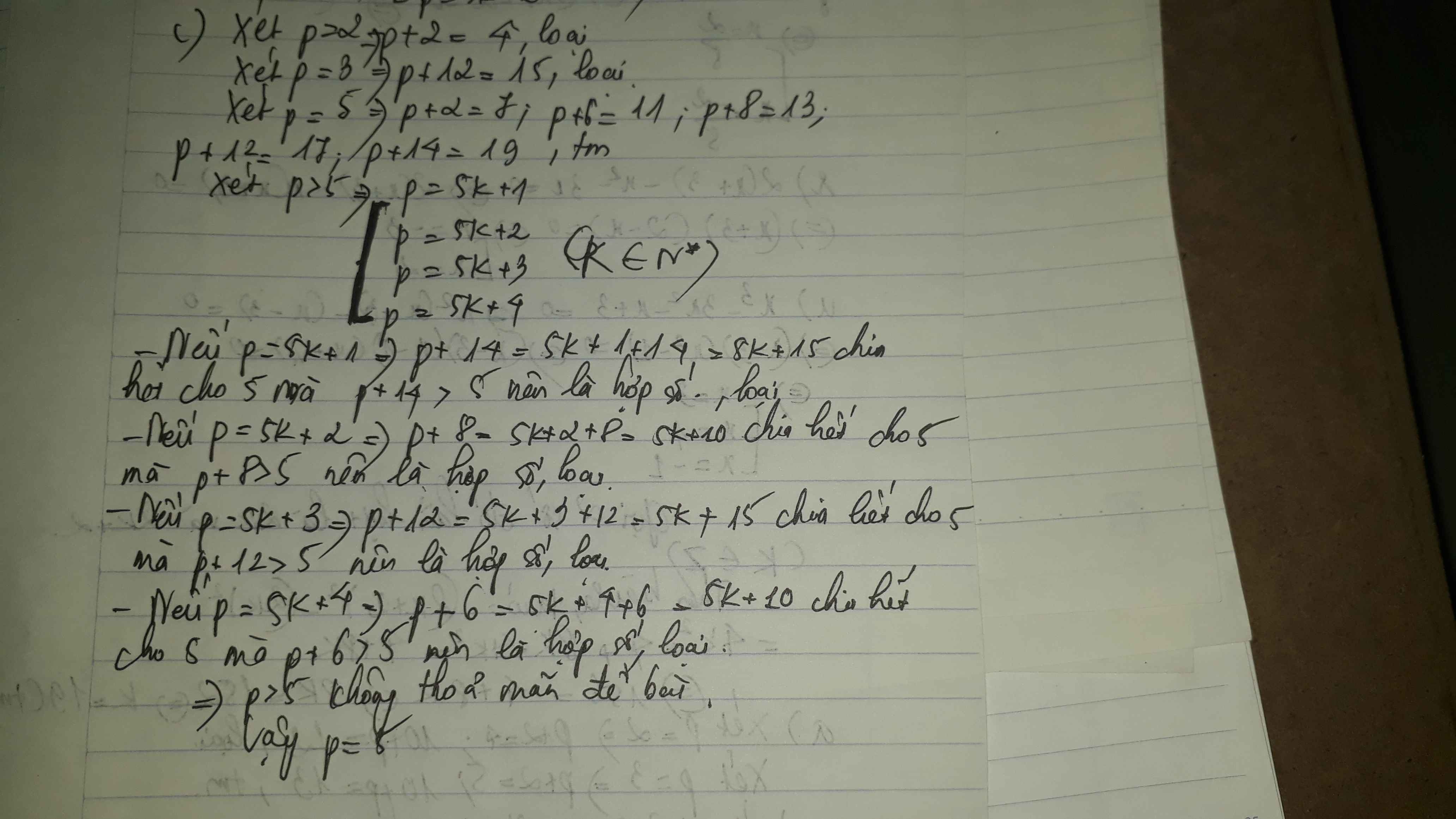
Bất kì số tự nhiên nào cũng có 1 trong các dạng: 3k; 3k +1; 3k + 2 (với k thuộc N)
- Với a = 3 thì a + 14 = 3 + 14 = 17 (thỏa mãn); a + 16 = 3 + 16 = 19 (thỏa mãn)
(ta xét cả trường hợp này vì k cũng có thể bằng 1)
- Với a = 3k thì a là hợp số (vì a còn chia hết cho 3) (loại)
- Với a = 3k + 1 thì a + 14 = 3k + 1 + 14 = 3k + 15 = 3(k + 5) là hợp số (loại)
- Với a = 3k + 2 thì a + 16 = 3k + 2 + 16 = 3k + 18 = 3(k+6) là hợp số (loại)
Vậy a = 3.
