Rút gọn: \(\left(\sqrt{21}+3\right)\sqrt{5-\sqrt{21}}-\sqrt{24}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
AH
Akai Haruma
Giáo viên
23 tháng 7 2021
Lời giải:
Đặt biểu thức là $A$. Ta có:
\(A=(5+\sqrt{21})(\sqrt{7}-\sqrt{3}).\sqrt{2}.\sqrt{5-\sqrt{21}}\)
\(=(5+\sqrt{21})(\sqrt{7}-\sqrt{3}).\sqrt{10-2\sqrt{21}}\)
\(=(5+\sqrt{21})(\sqrt{7}-\sqrt{3}).\sqrt{(\sqrt{7}-\sqrt{3})^2}\)
\(=(5+\sqrt{21})(\sqrt{7}-\sqrt{3})|\sqrt{7}-\sqrt{3}|=(5+\sqrt{21})(\sqrt{7}-\sqrt{3})^2\)
\(=(5+\sqrt{21})(10-2\sqrt{21})=2(5+\sqrt{21})(5-\sqrt{21})=2(5^2-21)=8\)
23 tháng 7 2021
Ta có: \(\left(5+\sqrt{21}\right)\cdot\left(\sqrt{14}-\sqrt{6}\right)\cdot\sqrt{5-\sqrt{21}}\)
\(=\dfrac{\left(10+2\sqrt{21}\right)\cdot\left(\sqrt{7}-\sqrt{3}\right)\cdot\sqrt{10-2\sqrt{21}}}{2}\)
\(=\dfrac{\left(\sqrt{7}+\sqrt{3}\right)^2\cdot\left(\sqrt{7}-\sqrt{3}\right)^2}{2}\)
=8
8 tháng 7 2018
\(\sqrt{3+\sqrt{5}}=\frac{\sqrt{6+2\sqrt{5}}}{\sqrt{2}}=\frac{\sqrt{5+2\sqrt{5}+1}}{\sqrt{2}}=\frac{\sqrt{\left(\sqrt{5}+1\right)^2}}{\sqrt{2}}=\frac{\sqrt{5}+1}{\sqrt{2}}\)
\(\sqrt{7+3\sqrt{5}}=\frac{\sqrt{14+2.3\sqrt{5}}}{\sqrt{2}}=\frac{\sqrt{9+2.3\sqrt{5}+5}}{\sqrt{2}}=\frac{\sqrt{\left(3+\sqrt{5}\right)^2}}{\sqrt{2}}=\frac{3+\sqrt{5}}{\sqrt{2}}\)
\(\sqrt{21+6\sqrt{6}}=\sqrt{3+2.\sqrt{3}.3\sqrt{2}+18}=\sqrt{\left(\sqrt{3}+3\sqrt{2}\right)^2}=\sqrt{3}+3\sqrt{2}\)
\(\sqrt{21-6\sqrt{6}}=\sqrt{18-2.3\sqrt{2}.\sqrt{3}+3}=\sqrt{\left(3\sqrt{2}-\sqrt{3}\right)^2}=3\sqrt{2}-\sqrt{3}\)
Nên \(E=\frac{\sqrt{5}+1+3+\sqrt{5}}{\sqrt{2}}.\left(3\sqrt{2}+\sqrt{3}+3\sqrt{2}-\sqrt{3}\right)\)
\(=\frac{4+2\sqrt{5}}{\sqrt{2}}.2.3.\sqrt{2}=24+12\sqrt{5}\)
4 tháng 10 2017
\(A=\)bn ghi lại đề nha mình lười
\(=\left(\sqrt{5+\sqrt{21}}\right)^2\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5-\sqrt{21}}\)
\(=\left(\sqrt{5+\sqrt{21}}\right)\left(\sqrt{5-\sqrt{21}}\right)\left(\sqrt{5+\sqrt{21}}\right)\left(\sqrt{14}-\sqrt{6}\right)\)
\(=\left(\sqrt{\left(5^2-21\right)}\right)\left(\sqrt{5+\sqrt{21}}\right)\left(\sqrt{14}-\sqrt{6}\right)\)
\(=2.\left(\sqrt{5+\sqrt{21}}\right)\sqrt{2}.\left(\sqrt{7}-\sqrt{3}\right)\)
\(=2.\left(\sqrt{10+2\sqrt{21}}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
\(=2.\left(\sqrt{7+2\sqrt{21}+3}\right) \left(\sqrt{7}-\sqrt{3}\right)\)
\(=2.\sqrt{\left(\sqrt{7}+\sqrt{3}\right)^2}\left(\sqrt{7}-\sqrt{3}\right)\)
\(=2.\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=2.\left(7-3\right)=2.4=8\)
tíck mình nha bn thanks nhìu !!!!!!!!!
HH
4 tháng 12 2020
Làm luôn nhé
\(2B=21.2\left[\left(\sqrt{2+\sqrt{3}}+\sqrt{3-\sqrt{5}}\right)-6\left(\sqrt{2-\sqrt{3}}+\sqrt{3+\sqrt{5}}\right)\right]^2-2.15\sqrt{15}\)
\(2B=21\left(\sqrt{3}+1+\sqrt{5}-1\right)^2-6\left(\sqrt{3}-1+\sqrt{5}-1\right)^2-30\sqrt{15}\)
\(2B=21\left(\sqrt{3}+\sqrt{5}\right)^2-6\left(\sqrt{3}+\sqrt{5}\right)^2-30\sqrt{15}\)
\(2B=15\left(\sqrt{3}+\sqrt{5}\right)^2-30\sqrt{15}\)
\(2B=15\left(8+2\sqrt{15}\right)-30\sqrt{15}\)
\(2B=120+30\sqrt{15}-30\sqrt{5}\)
\(2B=120\)
\(B=60\)
20 tháng 6 2021
`a)A=(3-sqrt5)sqrt{3+sqrt5}+(3+sqrt5)sqrt{3-sqrt5}`
`=sqrt{3-sqrt5}sqrt{3+sqrt5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt{9-5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=2(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt2(sqrt{6+2sqrt5}+sqrt{6-2sqrt5})`
`=sqrt2(sqrt{(sqrt5+1)^2}+sqrt{(sqrt5+1)^2})`
`=sqrt2(sqrt5+1+sqrt5-1)`
`=sqrt{2}.2sqrt5`
`=2sqrt{10}`
20 tháng 6 2021
`b)B=(5+sqrt{21})(sqrt{14}-sqrt6)sqrt{5-sqrt{21}}`
`=sqrt{5+sqrt{21}}sqrt{5-sqrt{21}}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=sqrt{25-21}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt2sqrt{5+sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{10+2sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{(sqrt3+sqrt7)^2}(sqrt{7}-sqrt3)`
`=2(sqrt3+sqrt7)(sqrt{7}-sqrt3)`
`=2(7-3)`
`=8`
`c)C=sqrt{4+sqrt7}-sqrt{4-sqrt7}`
`=sqrt{(8+2sqrt7)/2}-sqrt{(8-2sqrt7)/2}`
`=sqrt{(sqrt7+1)^2/2}-sqrt{(sqrt7+1)^2/2}`
`=(sqrt7+1)/sqrt2-(sqrt7-1)/2`
`=2/sqrt2=sqrt2`
28 tháng 6 2019
a. \(=\sqrt{2}.\left(\sqrt{7}+\sqrt{8}\right)\sqrt{5-\sqrt{3}\sqrt{7}}\)
\(=\left(\sqrt{7}+\sqrt{8}\right)\sqrt{3-2\sqrt{3}.\sqrt{7}+7}\)
\(=\left(\sqrt{7}+\sqrt{8}\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\)
\(=\left(\sqrt{7}+\sqrt{8}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
Rồi nhân ra. bạn làm tiếp nhé. Tuy nhiên minh nghĩ bạn bị nhầm đề. là \(\sqrt{6}\) chứ không phải căn 16
b. \(=\frac{5\left(\sqrt{21}+1\right)}{21-16}+\frac{\sqrt{3}.\sqrt{7}\left(\sqrt{3}-\sqrt{7}\right)}{-\left(\sqrt{3}-\sqrt{7}\right)}\)
\(=\sqrt{21}+4-\sqrt{21}=4\)
Tham khảo ạ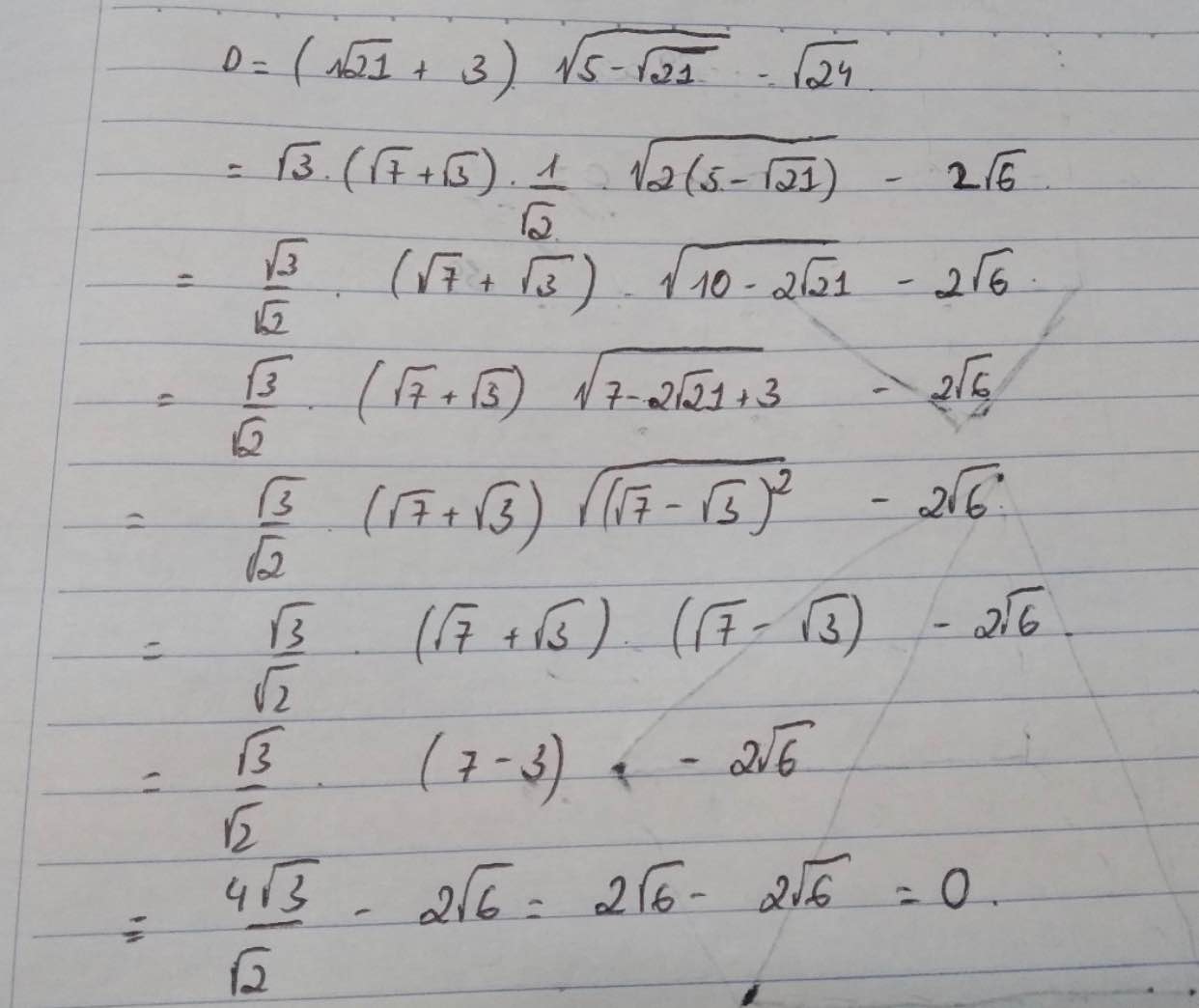
ở cái dấu = thứ 2 tại sao lại nhân với \(\dfrac{1}{\sqrt{2}}\) ạ?