
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số phần tử của không gian mẫu là n(Ω) = 10!.
Gọi A là biến cố mỗi học sinh đều nhận 1 đề và 2 bạn ngồi kề trên, dưới là khác loại đề.
Ta có:
Xếp 5 đề lẻ vào cùng 1 dãy ghế có 5! cách.
Xếp 5 đề chẵn vào cùng 1 dãy ghế có 5! cách.
Ở các cặp đề trên, dưới có thể đổi đề cho nhau nên có 2^5 cách.
=> n(A) = 5!.5!.2^5
Vậy P(A)=...
Lấy ngẫu nhiên 3 trong 5 đt là: 5C3 = 10 => n(Ω) = 10.Gọi A là biến cố 'chọn 3 đt có thể tạo được 1 tam giác.'Mà đk để tạo 1 tam giác là tổng 2 đoạn luôn lớn hơn đoạn còn lại.Do đó 5 đt thuộc {1,3,5,7,9} có bộ 3 thỏa mãn : {3,5,7} ; {3,7,9} ; {5,7,9}.=> n(A) = 3Vậy P(A) = 3/10

Chọn đáp án B
Phương pháp
Dựa vào đồ thị hàm số xác định các khoảng đơn điệu, các điểm cực trị và GTLN, GTNN của hàm số.
Cách giải
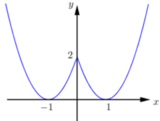
Dựa vào đồ thị hàm số ta thấy hàm số đã cho
+) Đồng biến trên (-1;0) và (1;+∞), nghịch biến trên (-∞;-1) và (0;1).
+) Hàm số có 3 điểm cực trị.
+) Hàm số không có GTLN.
Do đó các mệnh đề (I), (III) đúng.

Đáp án D
(I) Trên tập hợp các số phức thì phương trình bậc hai luôn có nghiệm.

Đáp án A
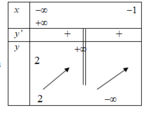
Phương pháp: Dựa vào BBT để kết luận tính đơn điệu của hàm số và suy ra các giá trị a, c tương ứng.
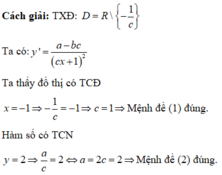
Theo BBT ta thấy hàm số đồng biến trên từng khoảng xác định của hàm số.
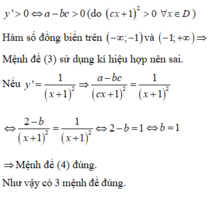

Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

* Hàm số đã cho liên tục trên R vì với 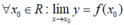 nên (1) đúng
nên (1) đúng
* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.
* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x
Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1
nên hàm số không có GTLN.
* Phương trình x 2 - 2 | x | + 2 = 0 vô nghiệm nên đồ thị không cắt trục hoành.
f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )
Nên hàm số đã cho là hàm số chẵn.
Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.
Chọn B
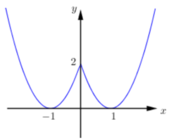



Ví dụ 9:
\(\hept{\begin{cases}x_A+x_B=2x_P\\x_B+x_C=2x_M\\x_C+x_A=2x_N\end{cases}}\Leftrightarrow\hept{\begin{cases}x_A+x_B=0\\x_B+x_C=2\\x_C+x_A=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x_A=1\\x_B=-1\\x_C=3\end{cases}}\)
\(\hept{\begin{cases}y_A+y_B=2y_P\\y_B+y_C=2y_M\\y_C+y_A=2y_N\end{cases}}\Leftrightarrow\hept{\begin{cases}y_A+y_B=-8\\y_B+y_C=2\\y_C+y_A=6\end{cases}}\Leftrightarrow\hept{\begin{cases}y_A=-2\\x_B=-6\\x_C=8\end{cases}}\)
Tọa độ các đỉnh của tam giác \(ABC\)là: \(A\left(1,-2\right),B\left(-1,-6\right),C\left(3,8\right)\).
Ví dụ 10:
\(\overrightarrow{AB}=\left(-1,6\right),\overrightarrow{AC}=\left(2,4\right)\)
\(\overrightarrow{CM}=2\overrightarrow{AB}-3\overrightarrow{AC}=\left(-2-6,12-12\right)=\left(-8,0\right)\)
Suy ra \(M\left(-5,2\right)\).