Tìm x,y thuộc Z
6xy - 3x - 12y - 24 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
18 tháng 7 2021
Đúng(0)
Những câu hỏi liên quan
CM
24 tháng 4 2019
Đáp án D
Cách giải
Vì d song song với hai mặt phẳng (P) và (Q) nên nhận
CM
21 tháng 8 2017
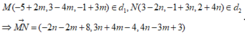
Chọn D
Cách giải : Vì d song song với hai mặt phẳng (P) và (Q) nên nhận
NT
0
3 tháng 9 2016
a/ Ta có : \(3y^2+12y+\left(4x^2+3x+5\right)=0\)
Xét \(\Delta'=6^2-3\left(4x^2+3x+5\right)=-12x^2-9x+21\)
Để pt trên có nghiệm thì \(\Delta'\ge0\Leftrightarrow-12x^2-9x+21\ge0\Leftrightarrow-\frac{7}{4}\le x\le1\)
Vì x là nghiệm nguyên nên \(0\le x\le1\)
Do đó x = 0 hoặc x = 1
Nếu x = 0 thì \(y_1=\frac{-6-\sqrt{21}}{3}\) (loại) , \(y_2=\frac{-6+\sqrt{21}}{3}\) (loại)
Nếu x = 1 thì y = -2 (nhận)
Vậy (x;y) = (1;-2)
3 tháng 9 2016
Đọc là "đen-ta" hay còn gọi là biệt thức. Bạn học sâu hơn về tam thức bậc hai (sách SGK 9 tập hai) để hiểu rõ hơn :)
NT
2
14 tháng 10 2019
A=3x2 + 9y2 - 6xy - 16x - 12y + 2049
3A=9x2 + 27y2 - 18xy - 48x - 36y + 6147
=(3x-3y-8)2+18y2-84y+6083
=(3x-3y-8)2+2.(3y-7)2+5985>5985
Dấu = xảy ra khi 3y-7=0 và 3x-3y-8=0=>y=7/3 và x=5=>3A=5985=>a=1995
Amin=1995<=>y=7/3 và x=5
mk chỉ tìm được GTNN thôi
