Cho phương trình : x3 + 2015x2 + 2016x + m = 0(m nguyên), có x0 là nghiệm hữu tỉ. C/tỏ rằng : x0 là số nguyên và m chia hết cho x0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
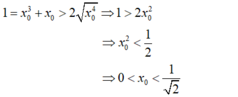

Chọn C.
Điều kiện x > 0.
Phương trình đã cho trở thành ![]()
![]()
![]()
Mà x0 được biểu diễn dưới dạng ![]() suy ra
suy ra 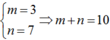

Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương ![]()
Lấy ln hai vế của , ta được ![]()
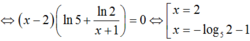
Suy ra x0 = 2 và P = 60.

2 x + m y = 1 m x + 2 y = 1 ⇔ y = 1 − m x 2 2 x + m 1 − m x 2 = 1 ⇔ y = 1 − m x 2 4 − m 2 x = 2 − m ⇔ y = 1 − m x 2 2 − m 2 + m x = 2 − m
Nếu m = 2 ⇒ 0x = 0 hệ phương trình có vô số nghiệm
Nếu m = − 2 ⇒ 0x = 4 hệ phương trình vô nghiệm
Nếu m ≠ ± 2 ⇒ ( 2 + m ) x = 1 x = 1 2 + m ⇒ y = 1 2 + m ⇒ M 1 2 + m ; 1 2 + m
Nhận thấy: M có tọa độ thỏa mãn tung độ = hoành độ
M nằm trên đường thẳng (d): x = y
Đáp án:C

=>2x+6y=2m+2 và 2x-y=7
=>7y=2m-5 và 2x-y=7
=>y=2/7m-5/7 và 2x=y+7
=>y=2/7m-5/7 và 2x=2/7m+30/7
=>x=1/7m+15/7 và y=2/7m-5/7
x0+2y0 bằng gì bạn ơi?

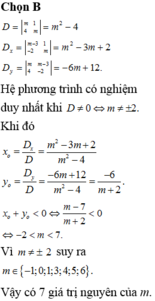
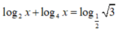
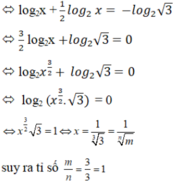
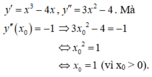
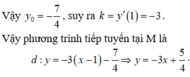
Vì \(x_0\) là số hữu tỉ nên ta có thể viết dưới dạng \(x_0=\frac{p}{q},\) với \(p,q\) nguyên tố cùng nhau, \(q>0\). Thay vào phương trình, rồi nhân cả hai vế với \(q^3\), ta được \(p^3+2015p^2q+2016pq^2+mq^3=0\to mq^3\vdots p,p^3\vdots q\to m\vdots p,q=1\to x_0=p\) là số nguyên.