Cho tam giác ABC . P , Q thứ tự là trung điểm của AB và AC qua C vẽ đường thẳng song song với AB cắt đường thẳng PQ tại D. Chứng minh rằng
a, Q là trung điểm của PD
b, PQ song song với BC và PQ = 1 / 2 BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

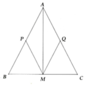
a) Vận dụng đinh lý 1 về đường trung bình của tam giác suy ra APMQ là hình thoi do có 4 cạnh bằng nhau.
b) Vì PQ ^ AM mà AM ^ BC (tính chất tamgiacs cân) nên PQ//BC.
a) xet tam giac AQP va tam giac CQD ta co
AQ=QC ( Q la trung diem AC)
goc AQP=goc CQD ( 2 goc doi dinh)
goc PAQ=goc QCD ( 2 goc so le trong va AB//CD)
--> tam giac AQP=tam giac CQD (g-c-g)
--> PQ=QD ( 2 canh tuong ung )
--> Q la trung diem PD
b) TA CO
AP=DC ( tam giac AQP=tam giac CQD)
AP=PB ( P la trung diem AB)
--> DC=PB
xet tam giac BPC va tam giac PCD ta co
DC=PB (cmt)
PC=PC ( canh chung)
goc DCP=goc BPC ( 2 goc so le trong va AB//CD)
--> tam giac BPC=tam giac PCD ( c-g-c)
--> goc BCP=goc DPC (2 goc tuong ung)
ma goc BCP va goc DPC nam o vi tri so le trong
nen PQ//BC
ta co
PD= BC ( tam giac PDC= tam giac BPC)
PQ=1/2 PD ( Q la trung diem PD)
-->PQ=1/2 BC