Phân tích thành nhân tử:
a) \(B=\left(4x+1\right)\left(12x-1\right)\left(12x-1\right)\left(x+1\right)-4\)
b) \(C=\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
c) \(D=\left(x^2+2x\right)^2+9x^2+18x+20\)
d) \(E=\left(x^2+3x+1\right)\left(x^2+3x+2\right)-6\)
e) \(F=\left(x^2+8x+7\right)\left(x+3\right)\left(x+5\right)+15\)

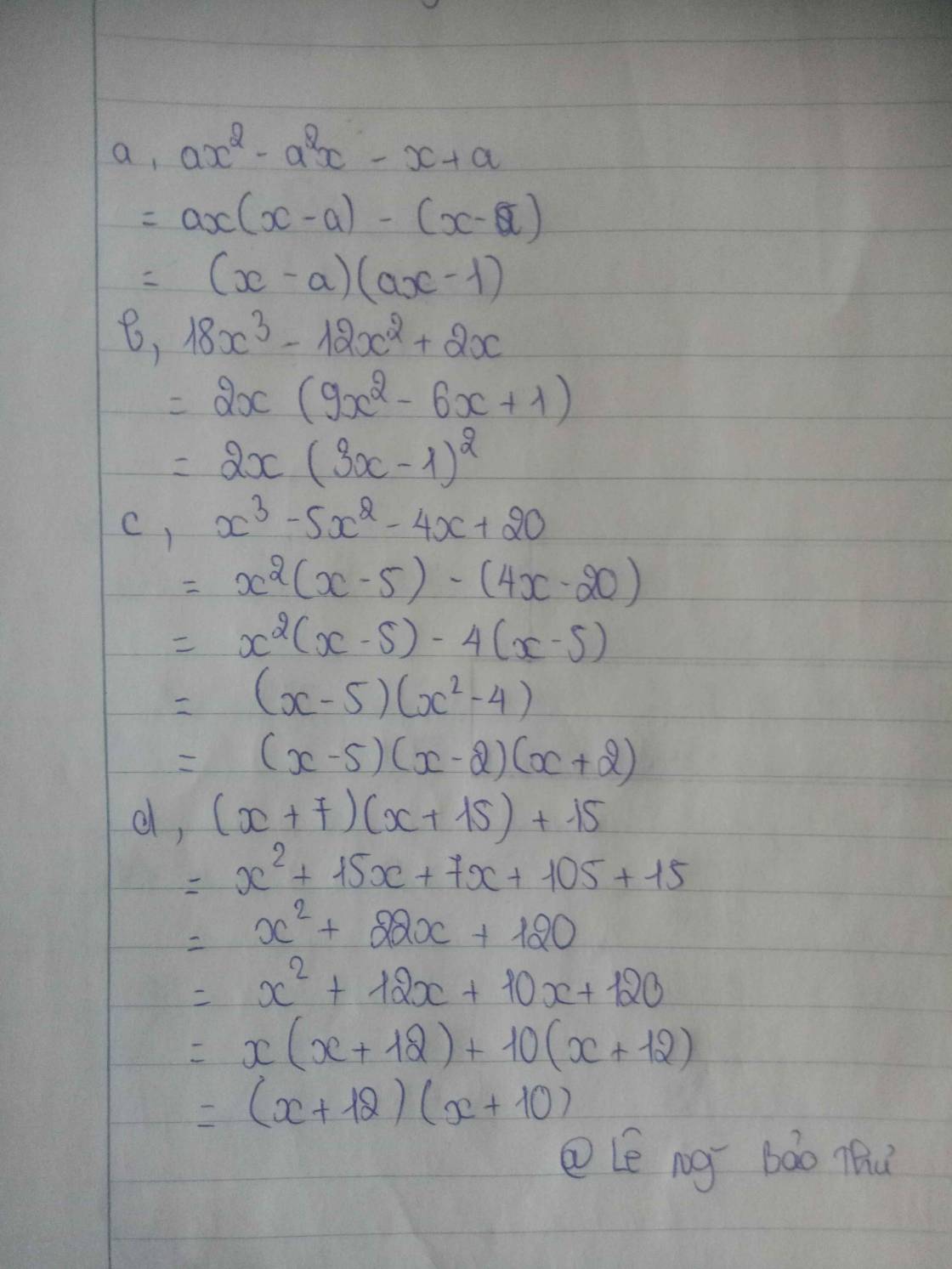
vào câu hỏi tương tự mà lm tương tự như thế nha