cho hình thang cân ABCD( AB // CD ) có góc A = 50 độ Tính góc B, C, D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PB
0
MN
9 tháng 7 2021
Bafi1: Do AB // CD ( GT )
⇒ˆA+ˆC=180o
⇒2ˆC+ˆC=180o
⇒3ˆC=180o
⇒ˆC=60o
⇒ˆA=60o.2=120o
Do ABCD là hình thang cân
⇒ˆC=ˆD
Mà ˆC=60o
⇒ˆD=60o
AB // CD ⇒ˆD+ˆB=180o
⇒ˆB=180o−60o=120o
Vậy ˆA=ˆB=120o;ˆC=ˆD=60o
MN
9 tháng 7 2021
Bài 2:
Ta có; AB//CD
\(\Rightarrow\)góc BAD+ góc ADC= \(180^o\)
^A=3. ^D \(\Rightarrow\)\(\dfrac{A}{3}\)=^D
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{A}{3}=\dfrac{D}{1}=\dfrac{A+D}{3+1}=\dfrac{180^O}{4}=45^O\)
\(\Rightarrow\)^A= \(135^O\)
\(\Rightarrow\)^D=\(45^o\)
\(\Rightarrow B=A=135^o\)
\(\Rightarrow C=D=45^o\)
LH
1
6 tháng 8 2018
Bạn tự vẽ hình nha:
Từ B kẻ đường thẳng vuông góc với DC cắt DC tại E
=> ABED là HCN vì có ba góc vuông
=> góc ABE = 90 độ
=> góc EBC= góc ABE - góc ABC = 90 - 50=30
Tam giác BCE có: góc BCE = 180 - góc CBE - góc BEC = 180-30 -90=60
=> góc BCD = 120 ( kề vs góc BCE)
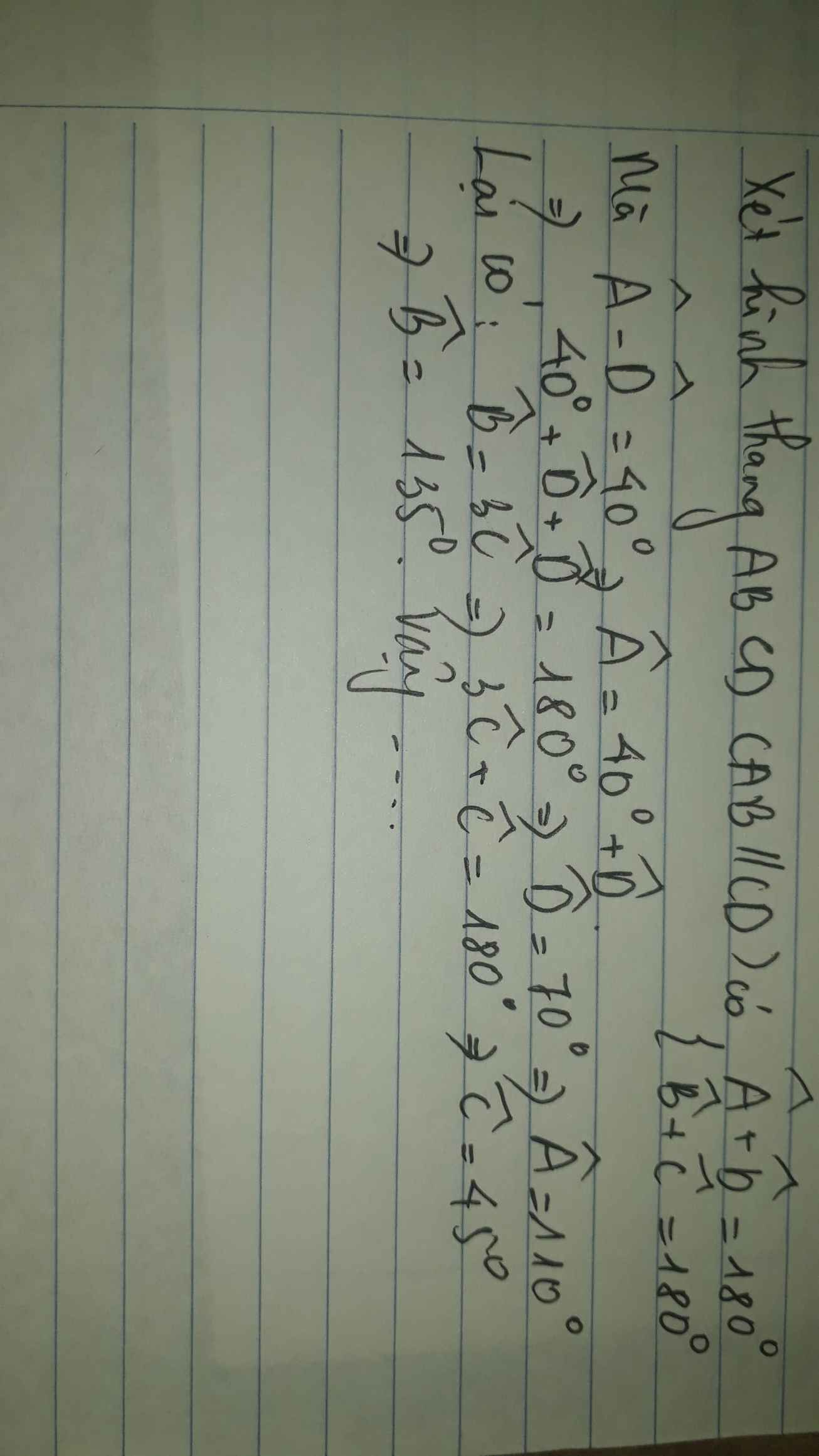
Ta có: ABCD là hình thang cân(gt)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)
\(\Leftrightarrow\widehat{D}+50^0=180^0\)
hay \(\widehat{D}=130^0\)
Ta có: ABCD là hình thang cân(Gt)
nên \(\widehat{A}=\widehat{B}\)(hai góc kề một đáy)
hay \(\widehat{B}=50^0\)
Ta có: ABCD là hình thang cân(gt)
nên \(\widehat{C}=\widehat{D}\)(hai góc kề một đáy)
hay \(\widehat{C}=130^0\)