Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, SA. Tìm giao tuyến của (MNP) vs các mp (SAB), (SAD), (SBC), (SCD).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
OP là đường trung bình tam giác BCD \(\Rightarrow OP//CD\)
Gọi Q là trung điểm SC \(\Rightarrow\) NQ là đường trung bình tam giác SCD \(\Rightarrow NQ//CD//OP\)
\(\Rightarrow NQ=\left(NPO\right)\cap\left(SCD\right)\)
Trong mp (SBD), nối NM kéo dài cắt SB tại G
\(\Rightarrow AG=\left(SAB\right)\cap\left(AMN\right)\)
Trong mp (ABCD), nối PM kéo dài cắt AD tại H
Trong mp (SAD), nối HN cắt SA tại E
\(\Rightarrow E=SA\cap\left(MNP\right)\)
Nhìn đi nhìn lại cũng ko biết ME//PN kiểu gì
Dễ dàng chứng minh EG=EN, mà GM=3MP nên ME không thể song song PN
Gọi F là giao điểm của MP và AB, I là giao điểm MP và CD
Trong mp (SCD), nối IN cắt SC tại J
Thiết diện là đa giác FENJP
HT
13 tháng 12 2020
P/s: Ngu phần hình ko gian nên chỉ giúp được thế này thôi nhó :)
23 tháng 2 2023
a: Xét hình thang ABCD có
M,N lần lượt là trung điểm của AB,CD
nên MN là đường trung bình
=>MN//AD//BC
=>MN//(SAD) và MN//(SBC)
b: Gọi giao của MN với BD là O
=>O thuộc (SBD) giao (MNP)
MP//SB
=>\(\left(SBD\right)\cap\left(MNP\right)=xy\left(O\in xy\right);\)xy//MP//SB
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Qua S kẻ đường thẳng d song song AD (và BC)
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)
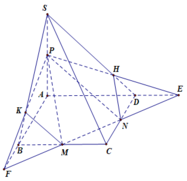
Trong mp (ABCD), nối MN kéo dài lần lượt cắt AB và AD kéo dài tại E và F
Trong mp (SAB), nối PE cắt SA tại G \(\Rightarrow PG=\left(MNP\right)\cap\left(SAB\right)\)
Trong mp (SAD), nối PF cắt SD tại H \(\Rightarrow PH=\left(MNP\right)\cap\left(SAD\right)\)
\(NH=\left(MNP\right)\cap\left(SCD\right)\)
\(GM=\left(MNP\right)\cap\left(SBC\right)\)
Sao biết PE cắt SA