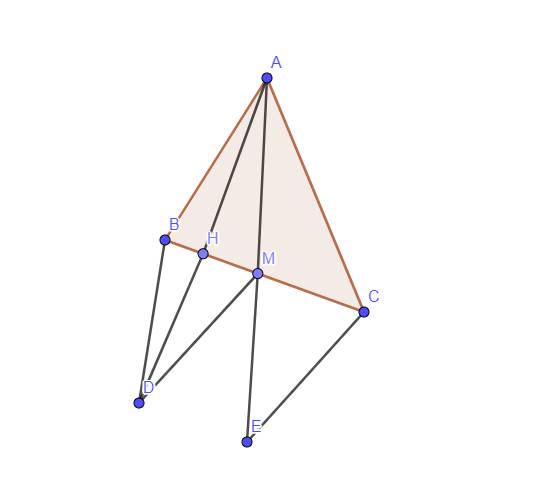
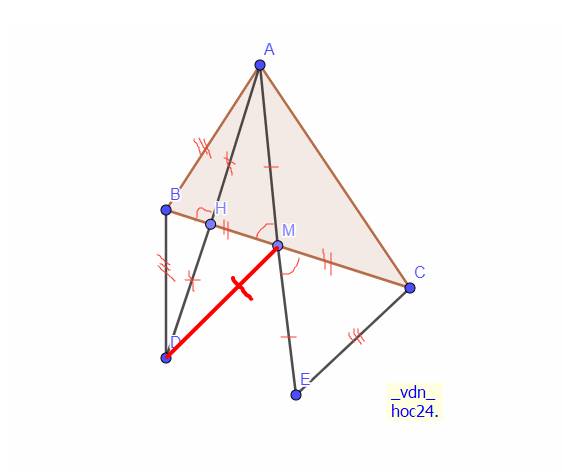
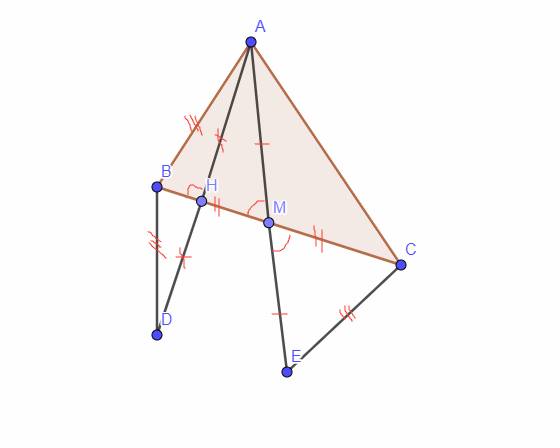
Cho tam giác ABC . Kẻ trung tuyến AM. Trên tia đối của tia MA lấy điểm E sao cho ME = MA
a)Cm tam giác ABM = tam giác ECM
b)Kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HD = HA Chứng minh BC là tia phân giác của góc ABD và BD = CE
c) Hai đường thẳng BD và CE cắt nhau tại K . Chứng Minh Tam gíac BCK cân

Cách 1: Giải theo phương pháp bậc tiểu học (của bạn Ác Quỷ)
Ta có
Mà dt(AMN) = 1/4 dt(ABN) = 1/4 . 1/2 dt(ABC) = 1/8 dt(ABC)
dt(DMN) = dt(ABC) - dt(AMN) - dt(BDM) - dt(CDN) = dt(ABC) - 1/8 dt(ABC) - 3/8 dt(ABC) - 1/4 dt(ABC) = 1/4 dt(ABC)
Vậy , suy ra AE/AD = 1/3
Cách 2: Giải theo phương pháp bậc THCS (của bạn Lê Quang Vinh)
DN là đường trung bình của tam giác ABC => DN // AB và DN = 1/2 AB
DN // AB => Hai tam giác EAM và EDN đồng dạng => EA/ED = AM/DN = 1/2 (vì AM = 1/4 AB, DN = 1/2 AB)
=> AE/AD = 1/3
cu lam nhu nguoi hoi nay lam dung 100 phan tram