Trên đường thẳng d lấy 3 điểm A,B,C ( C nằm giữa A và B).Trên cùng nửa mặt phẳng bờ là đường thẳng d.V ẽ tia Ax và By vuông góc với d. Trên tia By lấy N,tia vuông góc với NC tại C cắt Ax tại M. K ẻ CE vuông góc với MN tại E .Gọi I là trung điểm của CM. Chứng minh AM.BN=AC.BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 3 2018
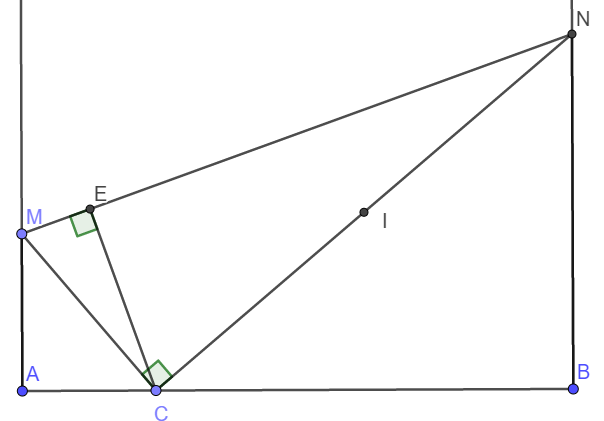
a) Tứ giác CENB có \(\widehat{CEN}=\widehat{CBN}=90^o\) nên bốn điểm B, C, E, N cùng thuộc đường tròn đường kính CN.
b) Ta có ngay \(\Delta MAC\sim\Delta CBN\left(g-g\right)\Rightarrow\frac{AM}{BC}=\frac{AC}{NB}\Rightarrow AM.BN=AC.BC\)
c) Ta có \(S_{AMNB}=\frac{\left(AM+BN\right).AB}{2}\)
Do AB, AM không đổi nên SAMNB lớn nhất khi và chỉ khi BN lớn nhất.
\(BN=\frac{AC.CB}{AM}\le\frac{\frac{\left(AC+CB\right)^2}{4}}{AM}=\frac{AB^2}{4AM}\)
Dấu bằng xảy ra khi \(AC=CB\) hay C là trung điểm AB.
30 tháng 12 2019
1) Có: \(\hept{\begin{cases}AM=MB\left(trungđiểm\right)\\\widehat{MAC}=\widehat{MBD}=90^o\\\widehat{AMC}=\widehat{BMD}\left(đốiđỉnh\right)\end{cases}}\Rightarrow\Delta AMC=\Delta BMD\left(g.c.g\right)\)
2) từ (1) suy ra: CM=DM; góc ACM=góc MDE(*)
CM đc: tam giác CME = tam giác DME ( c.g.c) (2)
Suy ra: góc MCE= góc MDE ( 2 góc tương ứng)(**)
từ (*) và (**) suy ra: góc ACM= góc MCE
Suy ra: CM là p/g .......
3) Từ (2) Có: CE=DE=DB+BE=AC+BE(ĐPCM)
Tam giác vuông AMC đồng dạng tam giác vuông BCN vì có góc AMC = góc BCN( vì cùng phụ góc ACM ). Suy ra AM/BC = AC/CN. Suy ra đpcm.