1. Cho HS y = x^3 -3x^2 +m. Với giá trị nào của m thì HS có cực đại , cực tiểu sao cho yCD và yCT trái dấu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y ' = x 2 - 2 m x + m 2 - 1
Dễ thấy rằng hàm số có hai điểm cực trị x = m + 1; x = m - 1 với mọi m
Ta có:
y C D + y C T > 2 ⇔ y m + 1 + y m - 1 > 2 ⇔ 2 m 3 - 2 m + 2 > 2 ⇔ - 1 < m < 0 m > 1
Đáp án A

\(y'=3x^2-2\left(2m-1\right)x+2-m\)
Hàm có các cực trị dương khi pt \(y'=0\) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(2m-1\right)^2-3\left(2-m\right)>0\\x_1+x_2=\dfrac{2\left(2m-1\right)}{3}>0\\x_1x_2=\dfrac{2-m}{3}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-m-5>0\\m>\dfrac{1}{2}\\m< 2\end{matrix}\right.\) \(\Rightarrow\dfrac{5}{4}< m< 2\)

Đáp án A
Xét hàm số y = x 3 - 2 x , ta có y ' = 3 x 2 - 2 ; y ' ' = 6 x
Phương trình
y ' = 0 ⇔ x 2 = 2 3 ⇔ x = ± 6 3 ⇒ y C T = - 4 6 9 y C D = 4 6 9 ⇒ y C T + y C D = 0

Đáp án C
Phương pháp:
+) Tính y’, giải phương trình y' = 0 ⇒ các cực trị của hàm số.
+) Tính các giá trị cực trị của hàm số và yCT.yCĐ < 0
Cách giải:
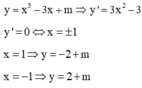
Giá trị cực đại và giá trị cực tiểu trái dấu ⇒ (-2 + m)(2 + m) < 0 ⇔ -2 < m < 2
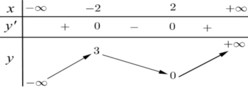

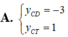
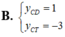

\(y'=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(\Rightarrow y_{CĐ}=y\left(0\right)=m\)
\(y_{CT}=y\left(2\right)=m-4\)
\(y_{CĐ}\) và \(y_{CT}\) trái dấu khi và chỉ khi:
\(m\left(m-4\right)< 0\Leftrightarrow0< m< 4\)