mọi người giúp em mấy bài này với ạ =(((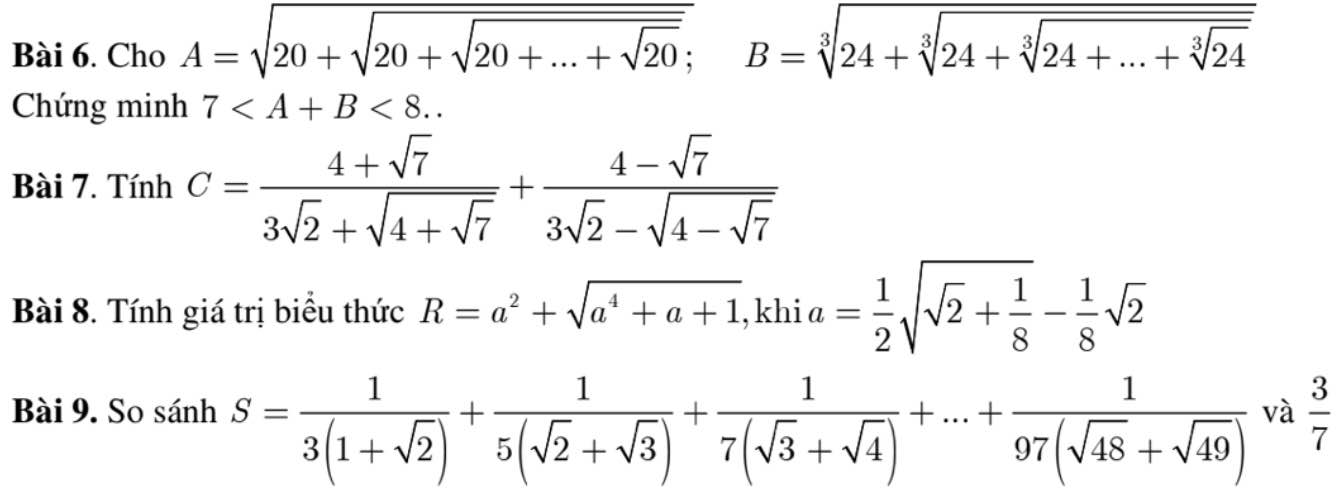
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 10 2021
8: Ta có: \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2
NT
1
2 tháng 12 2021
a) CuO + 2HCl → CuCl2 + H2O (1)
ZnO + 2HCl → ZnCl2 + H2O (2)
b) Gọi số mol CuO, ZnO lần lượt là x, y
mhh = mCuO + mZnO → 80x + 81y = 12,1 (*)
nHCl = 0,1 . 3 = 0,3 mol
Theo (1): nHCl (1) = 2nCuO = 2x
Theo (2): nHCl (2) = 2nZnO = 2y
nHCl = 2x + 2y = 0,3 (**)
Từ (*) và (**) → x = 0,05; y = 0,1
%mCuO=0,05.8012,1.100%=33,06%%mZnO=100%−33,06%=66,94%%mCuO=0,05.8012,1.100%=33,06%%mZnO=100%−33,06%=66,94%
c) CuO + H2SO4 → CuSO4 + H2O
0,05 → 0,05
ZnO + H2SO4 → ZnSO4 + H2O
0,1 → 0,1
nH2SO4 = 0,05 + 0,1 = 0,15 mol
mH2SO4 = 0,15 . 98 = 14,7g
mdd H2SO4 = 14,7 : 20% = 73,5(g)
cho mik xin 1 like zới đc khum:))
TD
2
Q
19 tháng 5 2021
vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
Bài 7:
Ta có: \(C=\dfrac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\dfrac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{6+\sqrt{8+2\sqrt{7}}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{6-\sqrt{8-2\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{7+\sqrt{7}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{7-\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{7}-1\right)\left(4+\sqrt{7}\right)}{6\sqrt{7}}+\dfrac{\sqrt{2}\left(\sqrt{7}+1\right)\left(4-\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(-3+3\sqrt{7}+3+3\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\sqrt{2}\)
6.
Ta có:
\(A=\sqrt{20+\sqrt{20+...+\sqrt{20}}}>\sqrt{20+\sqrt{\dfrac{1}{16}}}=\dfrac{9}{2}\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}>\sqrt[3]{24}=\sqrt[3]{\dfrac{192}{8}}>\sqrt[3]{\dfrac{125}{8}}=\dfrac{5}{2}\)
\(\Rightarrow A+B>\dfrac{9}{2}+\dfrac{5}{2}=7\)
\(A=\sqrt[]{20+\sqrt[]{20+...+\sqrt[]{20}}}< \sqrt[]{20+\sqrt[]{20+...+\sqrt[]{25}}}=5\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}< \sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{27}}}=3\)
\(\Rightarrow A+B< 5+3=8\)