hai tổ sản xuất cùng làm chung 1 công việc thì hoàn thành trong 6h. hỏi nếu làm riêng một mình thì mỗi tổ phải hết bao nhiêu thời gian mới hoàn thành cong việc, biết khi làm riêng tổ 1 hoàn thành sớm hơn tổ 2 5h
Gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
2 tháng 7 2021
Gọi thời gian tổ I hoàn thành là xx(h), khi đó thời gian tổ 2 hoàn thành là x+3x+3(h)
Khi đó, trong 1h thì tổ I và tổ II lần lượt làm đc là 1x1x(phần công việc) và 1x+31x+3 (phần công việc)
Do đó, trong 1h thì 2 tổ làm đc số phần công việc là 1x+1x+31x+1x+3(phần công việc)
Lại có 2 tổ làm chung thì hoàn thành công việc trong 2h, do đó trong 1h cả hai tổ làm đc 1212 (phần công việc). Do đó
1x+1x+3=121x+1x+3=12
⇒2(x+3)+2x=x(x+3)⇒2(x+3)+2x=x(x+3)
⇔x2−x−6=0⇔x2−x−6=0
⇔(x−3)(x+2)=0⇔(x−3)(x+2)=0
Vậy x=3x=3 hoặc x=−2x=−2(loại)
Suy ra x+3=6x+3=6
Vậy tổ I và tổ II làm trong 33(h) và trong 66(h) thì xong.
TD
2 tháng 7 2021
Viết nhầm: Câu cuối phải là: Vậy tổ 1 và tổ 2 làm trong 3 và 6 giờ thì xong
23 tháng 7 2015
* Giả sử nếu làm riêng thì tổ 1 hoàn thàn công việc trong x giờ => tổ 2 làm trong x + 3 giờ (do tổ 1 hoàn thành sớm hơn tổ 2 là 3 giờ mà)
* Do tổ 1 làm riêng thì hoàn thành cv trong x giờ nên mỗi giờ làm được 1/x công việc.
* Tương tự, tổ 2 mỗi giờ làm được \(\frac{1}{x+3}\) công việc.
* Nếu hai tổ củng làm thì mỗi giờ hoàn thành \(\frac{1}{x}\) + \(\frac{1}{x+2}\) công việc.
* Mặt khác, do cả hai tổ cùng là trong 2 giờ thì xong công việc nên mỗi giờ làm được \(\frac{1}{2}\)công việc.
Vậy ta có: \(\frac{1}{x}\) + \(\frac{1}{x+3}\) = \(\frac{1}{2}\) (quy đồng, nhân chéo rồi ra phương trình bậc 2, bạn tự làm nhé!!!)
=> x = 3.
Vậy nếu làm riêng tổ 1 hoàn thành công việc trong 3h, tổ 2 hoàn thành trong 6h
CM
23 tháng 3 2017
Gọi năng suất của tổ 1 là x (x > 6, phần công việc/giờ)
Vì hai tổ sản xuất cùng làm chung công việc thì hoàn thành trong 6 giờ nên năng suất của tổ 2 là: 1/6 – x (phần công việc/giờ);
Thời gian tổ 1 làm một mình xong công việc là: 1/x (giờ)
Thời gian tổ 2 làm một mình xong công việc là: 1 1 6 - x (giờ)
Vì khi làm riêng tổ một hoàn thành sớm hơn tổ hai là 5 giờ nên ta có phương trình:
Vậy thời gian tổ 1 hoàn thành công việc một mình là 10 giờ
Đáp án: B
CM
13 tháng 4 2017
Gọi năng suất của tổ 1 là x (x > 0, phần công việc/giờ)
Vì hai tổ sản xuất cùng làm chung công việc thì hoàn thành trong 2 giờ nên năng suất của tổ 2 là: ½ - x (phần công việc/giờ)
Thời gian tổ 1 làm 1 mình xong công việc là: 1/x (giờ)
Thời gian tổ 2 làm 1 mình xong công việc là: 1 1 2 - x (giờ)
Vì khi làm riêng, tổ một hoàn thành sớm hơn tổ hai là 3 giờ nên ta có phương trình:
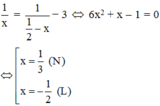
Vậy thời gian tổ 1 hoàn thành công việc một mình là 3 giờ
Đáp án: A
20 tháng 6 2021
gọi thời gian làm riêng của tô 2 là x(giờ)(x>2)
thì thời gian làm riêng của tổ 1 là x-3(h)
theo bài ra ta có pt: \(\dfrac{1}{x}+\dfrac{1}{x-3}=\dfrac{1}{2}=>x=6\left(TM\right)\)
Vậy tổ 2 làm riêng hết 6h
tổ 1 làm riêng hết 6-3=3 h
LT
20 tháng 6 2021
Gọi thời gian hoàn thành công việc một mình của tổ 2 là: x (giờ) (x > 2)
Thời gian hoàn thành công việc một mình của tổ 1 là: y (giờ) (y > 2)
Vì khi làm riêng tổ 1 hoàn thành sớm hơn tổ 2 là 3 giờ nên ta có phương trình:
x - y = 3 (1)
Trong 1 giờ:
Tổ 1 làm được: \(\dfrac{1}{y}\) (công việc)
Tổ 2 làm được: \(\dfrac{1}{x}\) (công việc)
Cả 2 tổ làm được: \(\dfrac{1}{2}\) (công việc)
Vì trong 1 giờ cả 2 tổ làm được \(\dfrac{1}{2}\) công việc nên ta có phương trình:
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\) (2)
Từ (1) và (2), ta có hệ phương trình:
\(\left\{{}\begin{matrix}x-y=3\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=y+3\\\dfrac{1}{y+3}+\dfrac{1}{y}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=y+3\\y^2-y-6=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=y+3\\\left[{}\begin{matrix}y=3\left(TM\right)\\y=-2\left(loại\right)\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=3\end{matrix}\right.\) (TM)
Vậy thời gian hoàn thành công việc một mình của tổ 2 là: 6 giờ.
Thời gian hoàn thành công việc một mình của tổ 1 là: 3 giờ.
DD
Đoàn Đức Hà
Giáo viên
27 tháng 5 2022
Cả hai tổ làm chung thì mỗi giờ làm được số phần công việc là:
\(1\div2=\dfrac{1}{2}\) (công việc)
Nếu làm riêng thì tổ 1 mỗi giờ làm hơn được tổ 2 số phần công việc là:
\(1\div3=\dfrac{1}{3}\) (công việc)
Nếu làm riêng mỗi giờ tổ 1 làm được số phần công việc là:
\(\left(\dfrac{1}{2}+\dfrac{1}{3}\right)\div2=\dfrac{5}{12}\) (công việc)
Nếu làm riêng mỗi giờ tổ 2 làm được số phần công việc là:
\(\dfrac{1}{2}-\dfrac{5}{12}=\dfrac{1}{12}\) (công việc)
Nếu làm riêng tổ 1 làm xong công viêc hết số giờ là:
\(1\div\dfrac{5}{12}=\dfrac{12}{5}\) (giờ)
Nếu làm riêng tổ 2 làm xong công việc hết số giờ là:
\(1\div\dfrac{1}{12}=12\) (giờ)
- Gọi thời gian làm một mình hết công việc của tổ 1 là x (h, x > 6 )
=> Một giờ tổ 1 hoàn thành số phần công việc là : \(\dfrac{1}{x}\) ( phần )
=> Thời gian làm riêng của tổ 2 là : x + 5 ( giờ )
=> Một giờ tổ 2 hoàn thành số phần công việc là : \(\dfrac{1}{x+5}\) ( phần )
Theo bài ra khi làm chung thì hai tổ hoàn thành trong 6 giờ .
\(\Rightarrow\dfrac{1}{x}+\dfrac{1}{x+5}=\dfrac{1}{6}\)
=> x = 10 ( TM )
Vậy thời gian làm riêng của tổ 1 và tổ 2 lần lượt là 10h và 15h .