Tìm các phân số lớn hơn 1/5 và không phải là số tự nhiên sao cho khi lấy tử số cộng với 2 và mẫu số nhân với 2 thì giá trị của phân số không đổi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2016
Gọi các phân số cần tìm có dạng là \(\frac{a}{b}\left(b\ne0\right)\)
Theo bài ra ta có \(\frac{a}{b}=\frac{a+3}{2b}\Leftrightarrow\frac{2a}{2b}=\frac{a+3}{2b}\Leftrightarrow2a=a+3\Leftrightarrow a=3\)
Khi đó:\(\frac{a}{b}=\frac{3}{b}>\frac{1}{5}\Leftrightarrow\frac{3}{b}>\frac{3}{15}\Leftrightarrow b< 15\)
Do a/b không là số tự nhiên nên a không chia hết cho b => \(b\ne1;3\)
Vậy các phân số cần tìm là 3/2;3/4;3/5;1/2;3/7;3/8;1/3;3/10;3/11;1/4;3/13;3/14
SY
2 tháng 6 2017
Gọi phân số đó là \(\frac{a}{b}\) .
Theo đề bài ta có:
\(\frac{a}{b}=\frac{a+2}{2b}\)
Mặt khác: \(\frac{a}{b}=\frac{2a}{2b}\)
Do đó: \(\frac{a+2}{2b}=\frac{2a}{2b}\)
\(\Rightarrow\) \(a+2=2a\)
\(\Rightarrow\) \(a=2\)
Ta phải tìm b để \(\frac{a}{b}=\frac{2}{b}>\frac{1}{5}\)
\(\Rightarrow\) \(\frac{2}{b}>\frac{2}{10}\)
Nên \(b< 10\)
Vậy \(b\in\left\{1;2;3;4;5;6;7;8;9\right\}\)
Mà \(\frac{a}{b}\) không phải là số tự nhiên.
Vậy các phân số cần tìm là \(\frac{2}{3};\frac{2}{4};\frac{2}{5};\frac{2}{6};\frac{2}{7};\frac{2}{8};\frac{2}{9}\)
31 tháng 1 2023
Gọi phân số là a/b
a/b = (a+2)/2b
=> 2ab=ab+2b
=> ab-2b=0
=> b=0 hoặc a=2
TH1: b=0 => loại
Th2: a=2 => mọi giá trị b
31 tháng 1 2023
Gọi số đó là a/b ta có :
a + 2/2 x b = a/b
a + 2/2 x b = 2 x a/2 x b
a + 2 = 2 x a
a + a = 2 x 2
2 x a = 4
a = 2
Vậy tử số của a là 2
Vì 2/b > 1/5
Mà 2/1 và 2/2 đều là số tự nhiên
nên ta có kết quả là:
2/3 ; 2/4 ; 2/5 ; 2/6 ; 2/7 ; 2/8 ; 2/9
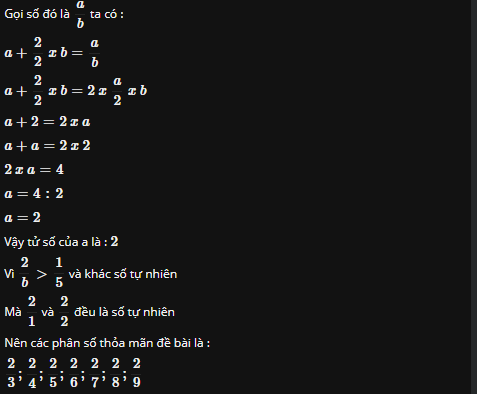
Gọi số đó là a/b ta có :
a + 2/2 x b = a/b
a + 2/2 x b = 2 x a/2 x b
a + 2 = 2 x a
a + a = 2 x 2
2 x a = 4
a = 4 : 2
a = 2
Vậy tử số của a là 2
Vì 2/b > 1/5 và khác số tự nhiên
Mà 2/1 và 2/2 đều là số tự nhiên
Nên các phân số thỏa mãn đề bài là :
2/3 ; 2/4 ; 2/5 ; 2/6 ; 2/7 ; 2/8 ; 2/9 .