6. Cho tam giác ABC vuông ở A đường cao AH, biết AB = 6cm, AC =8cm. a/ Tính AH; b/ Tính góc HAC; c/ Từ H kẻ HE AB, HF AC. Tính EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2021
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
HP
1
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
K
1
CM
2 tháng 12 2018
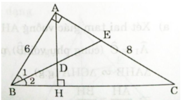
a) Ta có BE là phân giác của ∠ABC (gt)
⇒ ∠B1 = ∠B2
Do đó hai tam giác vuông:
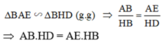
b) Ta có:
(định lý Pitago)
Xét hai tam giác vuông AHB và CAB có góc B chung nên :
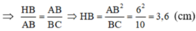
a)Áp dụng đl pytago ta có:
`BC^2=AB^2+AC^2=36+64=100`
`<=>BC=10cm`
Áp dụng HTL vào tam giác vuông ABC ta có:
`AH.BC=AB.AC`
`<=>10AH=48`
`<=>AH=4,8cm`
b)Xét tam giác vuông HAC ta có:
`cos hat{HAC}=(AH)/(AC)=3/5`
`=>hat{HAC}=53^o`
- Áp dụng định lý pitago vào tam giác ABC vuông tại A .
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
- Áp dụng hệ thức lượng vào tam giác vuông ABC đường cao AH .
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b, - Áp dụng tỉ số lượng giác vào tam giác HAC
Có : \(\cos A2=\dfrac{AH}{AC}=\dfrac{3}{5}\)
\(\Rightarrow\widehat{A2}\approx53^o\)15,
c, - Đề không rõ bạn ơi ;-;