Cho \(\Delta ABC\perp A\)đường cao AH. M,N là trung điêm của AB và AC . HM=15cm, HN=20cm. Tinh HB , HC , HA?
.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 6 2019
Xét \(\Delta HAC\)vuông tại H có HN là đường trung tuyến ứng với cạnh huyền
=> HN = NC = NA = AC/2
=> AC = 2HN = 8
Tương tự AB = 6
Theo hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A có AH là đường cao thì
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)
\(\Leftrightarrow AH=\frac{24}{5}\)
Áp dụng định lí Pytago vào \(\Delta HAC\)vuông tại H có
\(HA^2+HC^2=AC^2\)
\(\Leftrightarrow\left(\frac{24}{5}\right)^2+HC^2=8^2\)
\(\Leftrightarrow HC=\frac{32}{5}\)
Tương tự \(HB=\frac{18}{5}\)
CM
26 tháng 10 2019
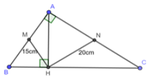
Xét ∆ ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = 1 2 AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ∆ ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = 1 2 AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D
HH
24 tháng 6 2018
Hình:
Giải:
a) Ta có:
\(AB>AC\left(gt\right)\)
\(\Leftrightarrow HB>HC\) (Quan hệ giữa hình chiếu và đường xiên)
b) Ta có: \(AB>AC\left(gt\right)\)
\(\Leftrightarrow\widehat{ABC}< \widehat{ACB}\) (Quan hệ cạnh và góc đối diện)
Lại có:
\(\widehat{BAH}+\widehat{ABC}+\widehat{AHB}=180^0\) (Tổng ba góc tam giác)
\(\Leftrightarrow\widehat{BAH}+\widehat{ABC}+90^0=180^0\)
\(\Leftrightarrow\widehat{BAH}=180^0-\widehat{ABC}-90^0\)
\(\Leftrightarrow\widehat{BAH}=900^0-\widehat{ABC}\)
Tương tự ta được:
\(\Leftrightarrow\widehat{CAH}=900^0-\widehat{ACB}\)
Ta có:
\(\widehat{ABC}< \widehat{ACB}\) (Chứng minh trên)
\(\Leftrightarrow-\widehat{ABC}>-\widehat{ACB}\)
\(\Leftrightarrow90^0-\widehat{ABC}>90^0-\widehat{ACB}\)
\(\Leftrightarrow\widehat{BAH}>\widehat{CAH}\)
c) Gọi I và K lần lượt là giao điểm của HN với AC và HM với AB
Xét tam giác AIN và tam giác AIH, có:
\(\widehat{AIN}=\widehat{AIH}=90^0\) (HN là đường trung trực của AC)
AI chung
\(IN=IH\) (HN là đường trung trực của AC)
\(\Rightarrow\Delta AIN=\Delta AIH\left(c.g.c\right)\)
\(\Rightarrow AN=AH\) (Hai cạnh tương ứng) (1)
Chứng minh tương tự với tam giác AKM và tam giác AKH, ta được:
\(\Delta AKM=\Delta AKH\left(c.g.c\right)\)
\(\Rightarrow AM=AH\) (Hai cạnh tương ứng) (2)
Từ (1) và (2) \(\Rightarrow AM=AN\) (Bắc cầu)
Suy ra tam giác MAN cân tại A
Vậy ...
PH
25 tháng 6 2018
bạn ơi câu b mình nghĩ bạn làm sai rồi hoặc là mình chưa hiểu, bạn giải thích cho mình đc ko
HH
7 tháng 9 2019
Xét tg ABH vuông tại H có Ma=MB=> MH là đường trung tuyến
=>MH=\(\frac{1}{2}\)AB=>AB=30cm
Xét tg AHC vuông tại H có AN=NC=>HN là đường trung tuyến
=>HN=\(\frac{1}{2}\)AC=>AC=40cm
Xét tg ABC vuông tại A có:
BC2=AB2+AC2(py-ta-go)
=>BC=50cm
Xét tg ABC có góc A=90o,đg cao AH ứng vs cạnh huyền BC.Aps dụng HTL tro tg vuông ta có:
AB2=BC.BH=>BH=18cm
Lại có:AC2=HC.BC=>HC=32cm
AH2=BH.HC =>AH=24cm
VM
30 tháng 10 2019
Tham khảo:
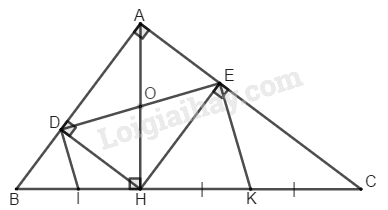
\(\Rightarrow\) Tứ giác \(DIEK\) là hình thang (định nghĩa hình thang) (đpcm).
Hình thang vuông là hình thang chỉ có 1 góc vuông thôi nhưng trong tứ giác \(DIEK\) có tận 2 góc vuông nên mình nghĩ chỉ suy ra là hình thang thôi.
Chúc bạn học tốt!
17 tháng 9 2021
b: Xét ΔAHC vuông tại H có
\(AC^2=AH^2+HC^2\)
hay \(AH^2=AC^2-HC^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AC^2-HC^2=AN\cdot AC\)
15 tháng 7 2016
tam giác AHB vuông tại H có HM là trung tuyến ứng với cạnh huyền AB=> HM=1/2AB=>AB=2HM=2.15=30cm
tam giác AHC vuông tại H có HN là trung tuyến ứng với cạnh huyền AC=>HN=1/2AC=>AC=2HN=2.20=40 cm
tam giác ABC vuông tại A =>\(BC^2=AB^2+AC^2suyraBC=\sqrt{AB^2+AC^2}=\sqrt{30^2+40^2}=50cm\)
ta có AH.BC=AB.AC=>AH=[30.40]/50=24cm hệ thức lượng tam giác vuông
ta có \(AB^2=BH.BCsuyraBH=\frac{AB^2}{BC}=\frac{30^2}{50}=18cm\)
suy ra HC=BC-BH=50-18=32cm
Tam giác AHB vuông tại H có HM là trung tuyến
=> HM = 1/2 AB => AB = 30 cm
Tam giác AHC vuông tại H có HN là trung tuyến
=> HN = 1/2 AC => AC = 40 cm
Áp dụng Pytago ta có: AB2 + AC2 = BC2
=> BC2 = 302 + 402 = 2500
=> BC = 50
Áp dụng hệ thức lượng ta có:
AB2 = BH.BC => \(BH=\frac{AB^2}{BC}=18\)
AC2 = CH.BC => \(CH=\frac{AC^2}{BC}=32\)
HA.BC = AB.AC => \(HA=\frac{AB.AC}{BC}=24\)