cho hình thang ABCD (AB//CD) .Gọi O là giao điểm của 2 đường chéo.
a) Qua O kẻ đường thẳng // AB cắt AD , BC theo thứ tự tại M và N . C/m : OM=ON
b) Đường thẳng // với AB bất kì cắt AD , AC ,BD,BC theo thứ tự tại P,Q,I,K . C/m : PQ=IK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Xét ΔADC có OM//DC
nen OM/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thag ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1) (2)và (3) suy ra OM=ON

Bài 2:
Xét ΔADC có OM//DC
nen OM/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thag ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1) (2)và (3) suy ra OM=ON

Sửa đề: Đường thẳng qua O song song với AB
Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
\(\widehat{BAO}=\widehat{DCO}\)(hai góc so le trong, AB//CD)
Do đó: ΔAOB\(\sim\)ΔCOD(g-g)
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{OA}{OB}=\dfrac{OC}{OD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{OA}{OB}=\dfrac{OC}{OD}=\dfrac{OA+OC}{OB+OD}=\dfrac{AC}{BD}\)
\(\Leftrightarrow\dfrac{OC}{OD}=\dfrac{AC}{BD}\)
\(\Leftrightarrow\dfrac{CO}{CA}=\dfrac{DO}{DB}\)(1)
Xét ΔDAB có
M∈AD(gt)
O∈BD(gt)
MO//AB(gt)
Do đó:\(\dfrac{DO}{DB}=\dfrac{MO}{AB}\)(Hệ quả của Định lí Ta lét)(2)
Xét ΔABC có
O∈AC(gt)
N∈BC(gt)
ON//AB(gt)
Do đó: \(\dfrac{CO}{CA}=\dfrac{ON}{AB}\)(Hệ quả của Định lí Ta lét)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{OM}{AB}=\dfrac{ON}{AB}\)
hay OM=ON(đpcm)
\(\Leftrightarrow OM+ON=MN=2\cdot ON\)
Xét ΔBCD có
O∈BD(gt)
N∈BC(gt)
ON//DC(gt)
Do đó: \(\dfrac{ON}{CD}=\dfrac{BN}{BC}\)(Hệ quả của Định lí Ta lét)(4)
Xét ΔABC có
O∈AC(gt)
N∈BC(gt)
ON//DC(gt)
Do đó: \(\dfrac{ON}{AB}=\dfrac{CN}{CB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{ON}{AB}+\dfrac{ON}{CD}=\dfrac{BN}{BC}+\dfrac{CN}{BC}=1\)
\(\Leftrightarrow\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{ON}=\dfrac{2}{2\cdot ON}=\dfrac{2}{MN}\)(đpcm)

+ Xét ΔOCD có AB // CD theo hệ quả định lý Ta-lét ta có :
\(\frac{OA}{AD}=\frac{OB}{BC}\)
+ Xét ΔACD có OM // CD theo hệ quả định lý Ta-lét ta có :
\(\frac{OM}{CD}=\frac{OA}{AD}=\frac{OB}{BC}\)
+ Xét ΔBCD có ON // CD ta có :
\(\frac{ON}{CD}=\frac{OB}{BC}=\frac{OM}{CD}\)
=> OM = ON

ta có
AB//CD do đó \(\frac{OA}{OD}=\frac{OB}{OC}\Rightarrow\frac{DA}{DO}=\frac{CB}{CO}\)
mà ta có \(\frac{AB}{MO}=\frac{CB}{CO}=\frac{DA}{DO}=\frac{AB}{NO}\Rightarrow MO=NO\)
vậy ta có đpcm

Trong ΔDAB, ta có: OM // AB (gt)
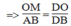 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
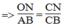 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: ![]() (định lí Ta-lét) (3)
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 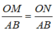
Vậy: OM = ON