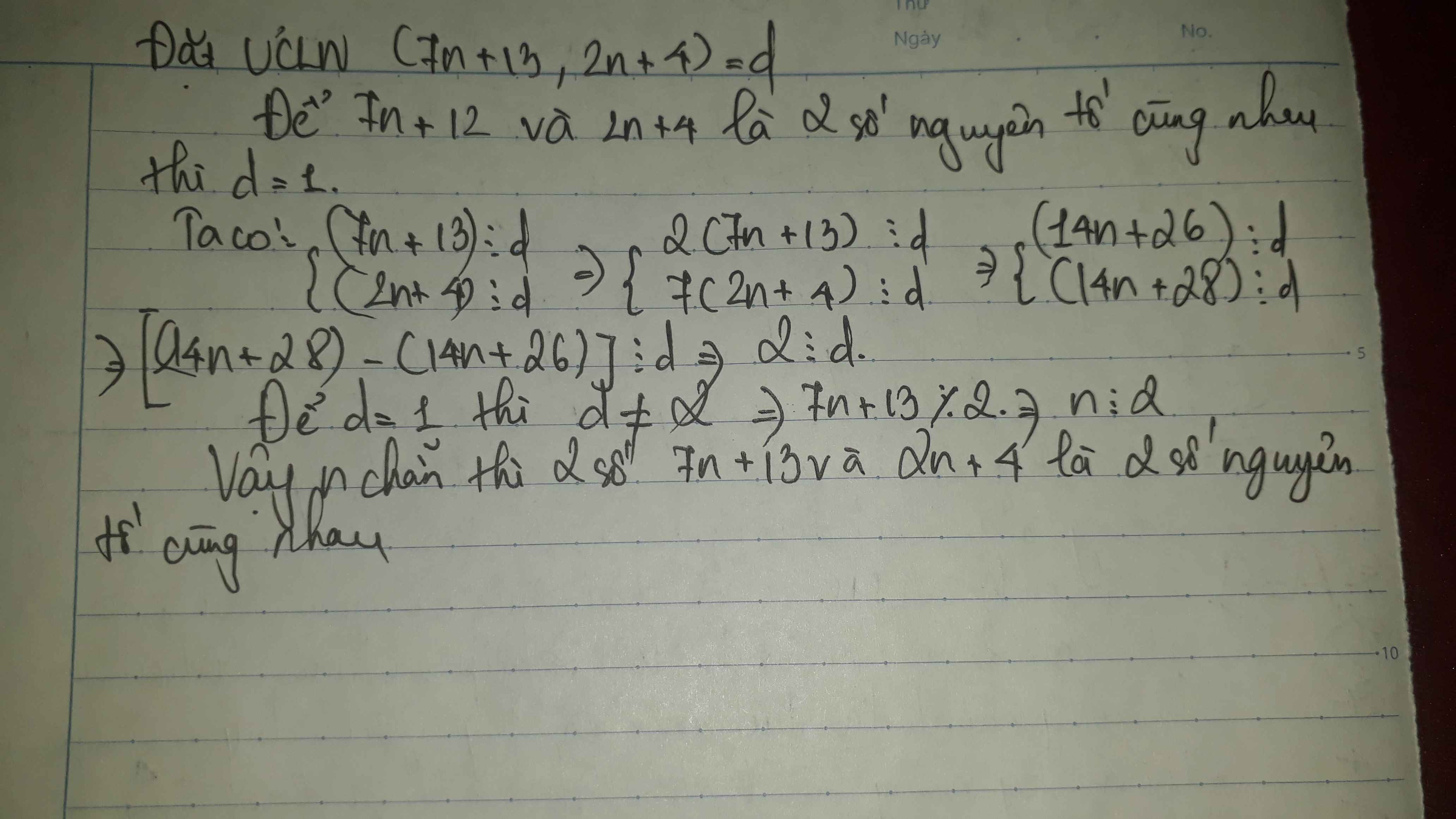Tìm số tự nhiên n để A= \(\frac{7n-8}{2n-3}\) là số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AK
1
31 tháng 3 2018
Đặt \(A=\frac{7n-8}{2n-3}\) ta có :
\(A=\frac{7n-8}{2n-3}=\frac{7}{2}.\frac{2\left(7n-8\right)}{7\left(2n-3\right)}=\frac{7}{2}.\frac{14n-16}{14n-21}=\frac{7}{2}.\left(\frac{14n-21}{14n-21}+\frac{5}{14n-21}\right)\)
\(A=\frac{7}{2}.\left(1+\frac{5}{14n-21}\right)=\frac{7}{2}+\frac{7.5}{2\left(14n-21\right)}=\frac{7}{2}+\frac{7.5}{7\left(4n-6\right)}=\frac{7}{2}+\frac{5}{4n-6}\)
Để A đạt GTLN thì \(\frac{5}{4n-6}\) phải đạt GTLN hay \(4n-6>0\) và đạt GTNN
\(\Rightarrow\)\(4n-6=1\)
\(\Rightarrow\)\(4n=7\)
\(\Rightarrow\)\(n=\frac{7}{4}\) ( loại vì n là số tự nhiên )
Do đó : \(4n-6=2\)
\(\Rightarrow\)\(4n=8\)
\(\Rightarrow\)\(n=2\)
Suy ra :
\(A=\frac{7n-8}{2n-3}=\frac{7.2-8}{2.2-3}=\frac{14-8}{4-3}=\frac{6}{1}=6\)
Vậy \(A_{max}=6\) khi \(n=2\)
Chúc bạn học tốt ~
PT
1
CM
7 tháng 3 2017
a, Gọi d = ƯCLN(7n+13;2n+4).
=>2(7n+13) ⋮ d; 7(2n+4) ⋮ d
=> [(14n+28) – (14n+6)] ⋮ d
=> 2 ⋮ d => d = {1;2}
Nếu d = 2 thì (7n+3) ⋮ 2 => [7(n+1)+6] ⋮ 2 => 7(n+1) ⋮ 2
Mà ƯCLN(7,2) = 1 nên (n+1) ⋮ 2 => n = 2k–1
Vậy để 7n+13 và 2n+4 nguyên tố cùng nhau thì n ≠ 2k–1
b, Gọi d = ƯCLN(4n+3;2n+3)
=> (4n+3) ⋮ d; 2(2n+3) ⋮ d
=> [(4n+6) – (4n+3)] ⋮ d
=> 3 ⋮ d => d = {1;3}
Nếu d = 3 thì (4n+3) ⋮ 3 => [3(n+1)+n] ⋮ 3 => n ⋮ 3 => n = 3k
Vậy để 4n+3 và 2n+3 nguyên tố cùng nhau thì n ≠ 3k
BV
1
11 tháng 3 2018
* Ta có: \(\frac{7n-8}{2n-3}\)= \(\frac{7}{2}\).\(\frac{2}{7}\).\(\frac{7n-8}{2n-3}\)=\(\frac{7}{2}\).\(\frac{14n-16}{14n-21}\)
=\(\frac{7}{2}\).\(\frac{14n-21+5}{14n-21}\)=\(\frac{7}{2}\).(1 +\(\frac{5}{14n-21}\))
=\(\frac{7}{2}\)+\(\frac{5}{4n-6}\)
*Để phân số đó có GTLN thì \(\frac{5}{4n-6}\)có GTLN.
=>4n-6 phải lớn hơn 0 và có GTNN.
*Nếu 4n -6 = 1 thì n =\(\frac{7}{4}\)
( ko thỏa mãn x thuộc N)
*Nếu 4n - 6 = 2 thì n = 2 ( thỏa mãn)
Vậy n = 2 thì phân số \(\frac{7n-8}{2n-3}\)có GTLN.
NQ
0
PM
2
30 tháng 4 2017
(7n-8)/(2n-3) = (7n - 21/2 + 5/2)/(2n - 3) = [(7/2)(2n-3) + 5/2]/(2n-3) = 7/2 + 5/(4n-6)
Phân số đã cho có GTLN khi 5/(4n-6) có GTLN, tức là khi 4n-6 có giá trị dương nhỏ nhất (với n là stn) hay n = 2
Trả lời : n = 2 (khi đó phân số có GTLN là 7/2 + 5/2 = 6)
5 tháng 1 2019
Đặt \(A=\frac{7n-8}{2n-3}\)
\(\Rightarrow2A=\frac{14n-16}{2n-3}\)
\(\Rightarrow2A=\frac{7.\left(2n-3\right)+5}{2n-3}\)
\(\Rightarrow2A=7+\frac{5}{2n-3}\)
ĐỂ \(A_{Max}\Rightarrow2.A_{Max}\Rightarrow\left(\frac{5}{2n-3}\right)_{Max}\)
=>\(2n-3\)là số nguyên dương nhỏ nhỏ nhất co thể
\(\Rightarrow2n-3=1\Rightarrow n=2\)
NT
1
TN
0
