Tìm nghiệm của đa thức
a) x2+11x-12
b) 2x2-7x+9
c) x2-12x+20
d) 4x2-13x+3
e) x2-8x-20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn cần viết đề bằng công thức toán để được hỗ trợ tốt hơn.

Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 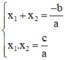
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 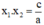
(Các bạn có thể làm cách 2 sử dụng điều kiện 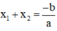 ).
).
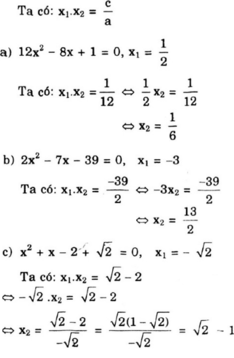
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0

a: \(x^2-6x+5=\left(x-5\right)\left(x-1\right)\)
b: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
c: \(x^2+8x+15=\left(x+5\right)\left(x+3\right)\)
d: \(2x^2-5x-12=\left(x-4\right)\left(2x+3\right)\)
e: \(x^2-13x+36=\left(x-9\right)\left(x-4\right)\)

b: 1/2x-4=0
=>1/2x=4
hay x=8
a: x+7=0
=>x=-7
e: 4x2-81=0
=>(2x-9)(2x+9)=0
=>x=9/2 hoặc x=-9/2
g: x2-9x=0
=>x(x-9)=0
=>x=0 hoặc x=9

a: x+7=0
nên x=-7
b: x-4=0
nên x=4
c: -8x+20=0
=>-8x=-20
hay x=5/2
d: x2-100=0
=>(x-10)(x+10)=0
=>x=10 hoặc x=-10

c. Ta có h(x) = 0 ⇒ 5x + 1 = 0 ⇒ x = -1/5
Vậy nghiệm của đa thức h(x) là x = -1/5 (1 điểm)

a: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)
b:\(=\dfrac{x^3+x^2+3x^2+3x+5x+5}{x+1}=x^2+3x+5\)
c:\(=\dfrac{x^3-3x^2-7x+2x^2-6x-14}{x^2-3x-7}=x+2\)
d: \(=\dfrac{x^2\left(x+5\right)+5x+25-25}{x+5}=x^2+5-\dfrac{25}{x+5}\)
a.\(x^2+11x-12\)
<=>\(x^2-x+12x-12\)
<=> \(x\left(x-1\right)+12\left(x-1\right)\)
<=> \(\left(x-1\right)\left(x+12\right)\)
b. \(2x^2-7x+9\)
Bài này mik kh pk lm, kh cs số nào nhân lại bằng 18 và cộng lại bằng -7 cả
c. \(x^2-12x+20\)
<=> \(x^2-2x-10x+20\)
<=> \(x\left(x-2\right)-10\left(x-2\right)\)
<=> \(\left(x-2\right)\left(x-10\right)\)
d. \(4x^2-13x+3\)
<=> \(4x^2-12x-x+3\)
<=> \(4x\left(x-3\right)-\left(x-3\right)\)
<=> \(\left(x-3\right)\left(4x-1\right)\)
e. \(x^2-8x-20\)
<=> \(x^2+2x-10x-20\)
<=> \(x\left(x+2\right)-10\left(x+2\right)\)
<=> \(\left(x+2\right)\left(x-10\right)\)