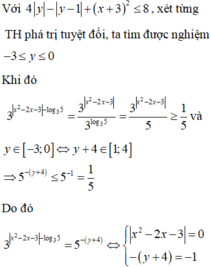Cho các số thực x, y thỏa mãn đồng thời các điều kiện x + 1/y = 3 ; y + 1/x = 4. Hãy tính giá trị biểu thức F = (x3y3) / (x6y6 +1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
1
MT
0
CM
13 tháng 9 2018
Chọn B.
Với 
,
xét từng TH phá dấu trị tuyệt đối, ta tìm được nghiệm
-3 ≤ y ≤ 0
Khi đó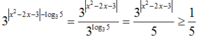 
và 
Do đó
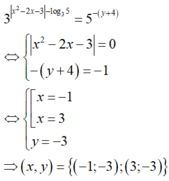
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
CM
4 tháng 7 2018
Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8 , xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0 .
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5 và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5 .
Do đó 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 ⇔ [ x = - 1 x = 3 y = - 3 ⇒ x ; y = - 1 ; - 3 ; 3 ; - 3 .
Vậy có tất cả hai cặp số thực (x;y) thỏa mãn yêu cầu bài toán.
CM
25 tháng 2 2019
Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8
xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5
và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5
Do đó
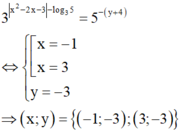
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
MT
1
31 tháng 8 2021
Ta có: \(\dfrac{x-1}{2}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
nên \(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
mà 2x+y-z=0
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}=\dfrac{2x+y-z-2+1+3}{4+3-5}=\dfrac{2}{2}=1\)
Do đó: x=3; y=2; z=8
