Chứng minh bất đẳng thức;
(a+b).(b+c).(c+a) > 8abc (a,b,c >0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
4
AH
Akai Haruma
Giáo viên
23 tháng 1 2022
Lời giải:
Bổ sung điều kiện $a,b$ là các số dương. Áp dụng BĐT Cô-si ta có:
$a+b\geq 2\sqrt{ab}$
$\frac{1}{a}+\frac{1}{b}\geq 2\sqrt{\frac{1}{ab}}$
$\Rightarrow (a+b)(\frac{1}{a}+\frac{1}{b})\geq 2\sqrt{ab}.2\sqrt{\frac{1}{ab}}=4$
Ta có đpcm
Dấu "=" xảy ra khi $a=b$
CM
26 tháng 6 2018
a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)
Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1
⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4
hay 5 < x4 + x3 + x2 + x + 1 < 5x4
⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)
hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)
b) x5 + y5 – x4y – xy4 = (x5 - x4y) - (xy4 - y5)
= x4.(x – y) – y4.(x – y)
= (x4 – y4).(x – y)
= (x2 + y2)(x2 – y2)(x – y)
= (x2 + y2).(x + y)(x – y)(x – y)
= (x2 + y2)(x + y)(x – y)2
Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0
⇒ x5 + y5 – x4y – xy4 ≥ 0.
c) Ta có: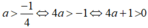 
Tương tự. 4b +1 >0 và 4c +1 > 0
Áp dụng bất đẳng thức Cô-si cho hai số dương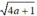 
và 1 ta có:
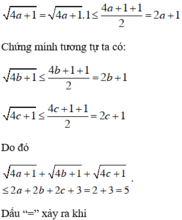
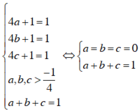
Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.
22 tháng 1 2022
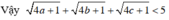
Coi như a, b, c là số dương
Áp dụng BĐT Cô-si ta có:
\(\dfrac{a}{bc}+\dfrac{c}{ba}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{c}{ba}}=2\sqrt{\dfrac{1}{b^2}}=\dfrac{2}{b}\left(1\right)\)
Dấu "=" xảy ra ...
\(\dfrac{a}{bc}+\dfrac{b}{ac}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{b}{ac}}=2\sqrt{\dfrac{1}{c^2}}=\dfrac{2}{c}\left(2\right)\)
Dấu "=" xảy ra ...
\(\dfrac{c}{ba}+\dfrac{b}{ac}\ge2\sqrt{\dfrac{c}{ba}+\dfrac{b}{ac}}=2\sqrt{\dfrac{1}{a^2}}=\dfrac{2}{a}\left(3\right)\)
Dấu "=" xảy ra ...
Từ (1), (2), (3) ta có:
\(\dfrac{a}{bc}+\dfrac{c}{ba}+\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ba}+\dfrac{b}{ac}\ge\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}\\ \Rightarrow2\left(\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ba}\right)\ge2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\\ \Rightarrow\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ba}\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Dấu "=" xảy ra ...
Vậy ...
CM
6 tháng 5 2018
a 3 b 3 = a 3 3 . b 3 3 = a b 3
Vế trái bằng vế phải nên đẳng thức được chứng minh.
7 tháng 3 2022
Thì bạn lấy một ví dụ đơn giản là A đi qua nhà B thì có hai cách là đi thẳng hoặc đi vòng. Nếu đi vòng thì độ dài quãng đường sẽ lớn hơn đi thẳng nên ta có bất đẳng thức tam giác
vì a>0;b>0;c>0\(\Rightarrow\sqrt{a};\sqrt{b};\sqrt{c}\)luôn được xác định
\(\left(\sqrt{a}-\sqrt{b}\right)^2>=0\Rightarrow a-2\sqrt{ab}+b>=0\Rightarrow a+b>=2\sqrt{ab}\)
\(\left(\sqrt{b}-\sqrt{c}\right)^2>=0\Rightarrow b-2\sqrt{bc}+c>=0\Rightarrow b+c>=2\sqrt{bc}\)
\(\left(\sqrt{c}-\sqrt{a}\right)^2>=0\Rightarrow c-2\sqrt{ca}+a>=0\Rightarrow c+a>+2\sqrt{ca}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)>=2\sqrt{ab}\cdot2\sqrt{bc}\cdot2\sqrt{ca}=8\sqrt{a^2b^2c^2}=8abc\)(đpcm)
dấu = xảy ra khi a=b=c
Áp dụng ĐBT Cauchy - schwarz cho 2 số không âm, ta được:
\(a+b\ge2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
\(a+c\ge2\sqrt{ac}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}=8abc\left(đpcm\right)\)