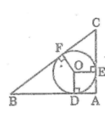
Cho tam giác ABC nội tiếp (O) (AB<AC) và đường cao AD. Vẽ đường kính AE của (O).
a) Chứng minh hai tam giác ADB và ACE đồng dạng và AD.AE=AB.AC
b) Vẽ dây AF của (O) song song với BC, FE cắt AC tại Q, BF cắt AD tại P.
Chứng minh PQ//BC
c) AE cắt BC tại K. Chứng minh AB.AC - AD.AK= \(\sqrt{BD.BK.CD.CK}\)
d) Các tiếp tuyến của (O) tại B và C cắt nhau tại I, AI cắt cung nhỏ BC tại H. Khi A di động trên (O) và BC cố định.
Chứng minh FH luôn đi qua một điểm cố định.
Mọi người giúp mình phần b) c) d) với ạ. Mình cảm ơn