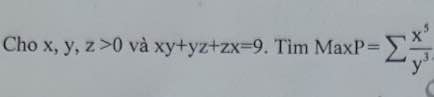Cho x+y+z=6 và xy+yz+zx=9.CMR: 0<=x<=4/3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
0
AH
Akai Haruma
Giáo viên
26 tháng 1 2021
Lời giải:
Áp dụng BĐT AM-GM:
\(\sqrt{\frac{xy}{xy+z}}=\sqrt{\frac{xy}{xy+z(x+y+z)}}=\sqrt{\frac{xy}{(z+x)(z+y)}}\leq \frac{1}{2}\left(\frac{x}{x+z}+\frac{y}{z+y}\right)\)
Hoàn toàn tương tự với các phân thức còn lại suy ra:
\(\sum \sqrt{\frac{xy}{xy+z}}\leq \frac{1}{2}\left(\frac{x+z}{x+z}+\frac{y+z}{y+z}+\frac{x+y}{x+y}\right)=\frac{3}{2}\)
Ta có đpcm.
Dấu "=" xảy ra khi $x=y=z=\frac{1}{3}$
HN
Cho x, y, z > 0 và x+y+z=1.
CMR : \(\dfrac{1-x^2}{x+yz}+\dfrac{1-y^2}{y+zx}+\dfrac{1-z^2}{z+xy}\ge6\)
0
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 7 2021
Nếu biểu thức là: \(P=\dfrac{x^5}{y^3}+\dfrac{y^5}{z^3}+\dfrac{z^5}{x^3}\) thì đề bài sai
Biểu thức này chỉ có min, không có max
