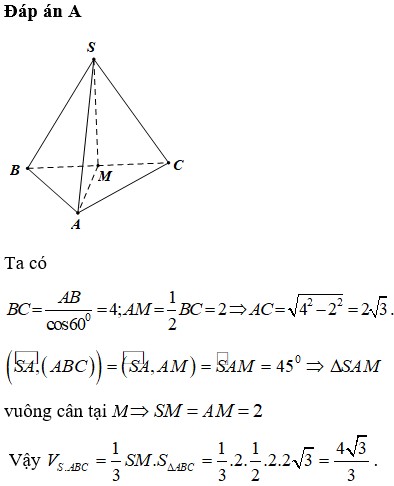
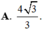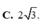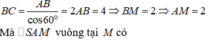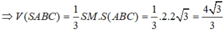Giải giúp mình:cho hình chóp SABC có đáy là tam giác đều cạnh 2a, hình chiếu của S lên ABC là trung điểm AB. Góc giữa SC và (ABC) là 60°. Tính VSABC/a³ là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều SBC cạnh a)
\(AH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều ABC cạnh a)
\(tan\widehat{SAH}=\dfrac{SH}{AH}=1\Rightarrow\widehat{SAH}=45^0\)

Đáp án D
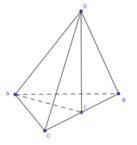
Góc giữa cạnh SA và đáy là SAF ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
A F = 3 2 a ; S F = 3 2 a
Vậy tan S A F ^ = 1 ⇒ S A G ^ = 45 0