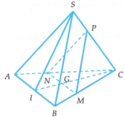
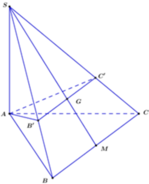
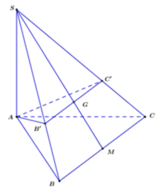
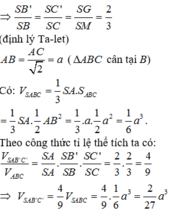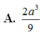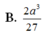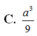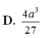Cho hình chóp tam giác S.ABC, điểm G là trọng tâm của tam giác SBC. Gọi K là trung điểm của SA. hãy xác định giao điểm của đường thẳng KG và mặt phẳng (ABC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 5 2021
a) \(SB^2=AS^2+AB^2=AS^2+AC^2=SC^2\Rightarrow SB=SC\) => \(\Delta\)SBC cân tại S
Do đó: AO,SH cắt nhau tại trung điểm I của cạnh BC
Xét \(\Delta\)SBC: trực tâm H, đường cao SI => \(IH.IS=IB.IC\)(1)
Tương tự: \(IB.IC=IO.IA\)(2)
Từ (1);(2) => \(IH.IS=IO.IA\)=> \(\Delta\)IHO ~ \(\Delta\)IAS => ^IHO = ^IAS = 900 => OH vuông góc IS (3)
Ta có: BC vuông góc với AI,AS => BC vuông góc với (SAI) => BC vuông góc OH (4)
Từ (3);(4) => OH vuông góc (SBC).
b) Xét tam giác SKI: IO vuông góc SK tại A, KO vuông góc SI tại H (cmt) => O là trực tâm tam giác SKI
Vậy SO vuông góc IK.
CM
31 tháng 1 2017
Đáp án D
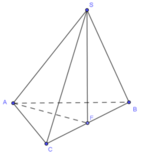
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
Vậy 
CM
14 tháng 10 2017
Chọn đáp án D
Ta có
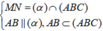
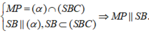
Khi đó 
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
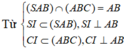
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0
