Một số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m.
Ví dụ: Số 1543 có tổng các chữ số bằng 1 + 5 + 4 + 3 = 13. Số 13 chia 9 dư 4 chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9, cho 3: 1546; 1527; 2468; 1011

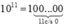 có tổng các chữ số bằng 1. 1 chia 3 và 9 đều dư 1.
có tổng các chữ số bằng 1. 1 chia 3 và 9 đều dư 1.
- Số 1546 có tổng 1 + 5 + 4 + 6 = 16. Tổng này chia cho 9 dư 7, chia cho 3 dư 1.
Do đó, số 1546 chia cho 9 dư 7, chia cho 3 dư 1.
- Số 1527 có tổng 1 + 5 + 2 + 7 = 15. Tổng này chia cho 9 dư 6, và chia hết cho 3.
Do đó, số 1527 chia cho 9 dư 6, và chia hết cho 3.
- Số 2468 có tổng 2 + 4 + 6 + 8 = 20. Tổng này chia cho 9 dư 2, chia cho 3 dư 2.
Do đó, số 2468 chia cho 9 dư 2, chia cho 3 dư 2.
- Số 1011 có tổng 1 + 0 + ... + 0 = 1. Tổng này chia cho 9 dư 1, chia cho 3 dư 1.
Do đó, số 1011 chia cho 9 dư 1, chia cho 3 dư 1.
Số 1546 = 1 + 5 + 4 + 6 = 16 : 9 dư 7 và chia 3 dư 1.
Vậy 1546 chia cho 9 dư 7 và chia cho 3 dư 1
Số 1527 = 1 + 5 + 2 + 7 = 15 : 9 dư 6 và chia hết cho 3.
Vậy 1527 chia hết cho 3 và chia 9 dư 6
Số 2468 = 2 + 4 + 6 + 8 = 20 : 9 dư 2 và chia 3 dư 2
Vậy 2468 đều dư 2 khi chia cho 3 và 9.
Số 10^11 có dạng là 100……000 và tổng này luôn luôn chia cho 3 và 9 đều dư 1
Vậy 10^11 chia cho 3 và 9 đều dư 1