cho đa thức p(x)=ax^3+bx^2+cx+d với a,b,c,d là các số nguyên biết P(0) vàP(1) là các số lẻ cmr P(x) không thể có nghiệm nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi nghiệm nguyên của P(x) là: k
ta có: ak3+bk2+ck+d=0ak3+bk2+ck+d=0
k.(ak2+bk+k)=−dk.(ak2+bk+k)=−d( *)
ta có: P(1)=a+b+c+dP(1)=a+b+c+d
P(0)=dP(0)=d
mà P(1); P(0) là các số lẻ
=> a+b+c+d và d là các số lẻ
mà d là số lẻ
=> a+b+c là số chẵn
Từ (*) => k thuộc Ư(d)
mà d là số lẻ
=> k là số lẻ
=> k3−1;k2−1;k−1k3−1;k2−1;k−1là các số chẵn
⇒a(k3−1)+b(k2−1)+c(k−1)⇒a(k3−1)+b(k2−1)+c(k−1) là số chẵn
=(ak3+bk2+ck)−(a+b+c)=(ak3+bk2+ck)−(a+b+c)
mà a+b+c là số chẵn
⇒ak3+bk2+c⇒ak3+bk2+c là số chẵn
Từ (*) => d là số chẵn ( vì d là số lẻ)
=> P(x) không thể có nghiệm nguyên

Ko biết là bạn có cần nữa ko.
Nhưng mình vẫn trả lời cho những bạn khác đang cần.
Do P(0) và P(1) lẻ nên ta có:
P(0)=d=> d là số lẻ
P(1)=a+b+c+d => a+b+c+d là số lẻ
Giả sử y là nghiệm nguyên của P(x). Khi đó:
P(y)=ay^3+by^2+cy+d=0
=>ay^3+by^2+cy=-d
Mà d là số lẻ
=>y là số lẻ
Lại có: P(y)-P(1)=(ay^3+by^2+cy+d)-(a+b+c+d)
=a(y^3-1)+b(y^2-1)+c(y-1)+(d-d)
=a(y^3-1)+b(y^2-1)+c(y-1)
Do y là số lẻ=>P(y)-P(1) là số chẵn(1)
Mà P(y)-P(1)= 0-a+b+c+d
=-a-b-c-d
Do a+b+c+d lẻ
=>-a-b-c-d lẻ
Hay P(y)-P(1) là số lẻ(2)
Vì (1) và (2) mâu thuẫn
=> Giả sử sai
Hay f(x) ko thể có nghiệm là các số nguyên(ĐCCM)

Làm hơi dài dòng tẹo nhé
f(0)=d là số lẻ
f(1)=a+b+c+d là số lẻ => a+b+c là số chẵn
Giả sử nghiệm x chẵn => f(x) lẻ khác 0 => loại
Giả sử nghiệm x lẻ
=> Tính chẵn lẻ của ax3 phụ thuộc vào a
Tính chẵn lẻ của bx2 phụ thuộc vào b
Tính chẵn lẻ của cx phụ thuộc vào c
d là số lẻ
Mà a+b+c là số chẵn=> ax3+bx2+cx là số chẵn => ax3+bx2+cx+d là số lẻ khác 0
Vậy f(x) không thể có nghiệm nguyên
Hơi khó hỉu chút nhé ahihi

Mấy cái này mk kho bít sorry!!!!!!253564656464646474748949474626515466575757575665555


\(2,\\ PT\Leftrightarrow6x^2+9y^2-\left(x^2+y^2\right)=20412\\ \text{Mà }20412⋮3;6x^2+9y^2⋮3\\ \Leftrightarrow x^2+y^2⋮3\Leftrightarrow x^2⋮3;y^2⋮3\Leftrightarrow x⋮3;y⋮3\)
Đặt \(\left\{{}\begin{matrix}x=3a\\y=3b\end{matrix}\right.\left(a,b\in Z\right)\Leftrightarrow5\left(3a\right)^2+8\left(3b\right)^2=20412\)
\(\Leftrightarrow9\left(5a^2+8b^2\right)=20412\\ \Leftrightarrow5a^2+8b^2=2268\)
Mà \(2268⋮3\Leftrightarrow5a^2+8b^2⋮3\Leftrightarrow a^2⋮3;b^2⋮3\Leftrightarrow a⋮3;b⋮3\)
Đặt \(\left\{{}\begin{matrix}a=3c\\b=3d\end{matrix}\right.\left(c,d\in Z\right)\Leftrightarrow9\left(5c^2+8d^2\right)=2268\Leftrightarrow5c^2+8d^2=252\)
Mà \(252⋮3\Leftrightarrow5c^2+8d^2⋮3\Leftrightarrow c^2⋮3;d^2⋮3\Leftrightarrow c⋮3;d⋮3\)
Đặt \(\left\{{}\begin{matrix}c=3k\\d=3q\end{matrix}\right.\left(k,q\in Z\right)\Leftrightarrow9\left(5k^2+8q^2\right)=252\Leftrightarrow5k^2+8q^2=28\)
\(\Leftrightarrow5k^2=28-8q^2\ge0\Leftrightarrow q^2\le\dfrac{28}{8}=3,5\\ \text{Mà }q\in Z\\ \Leftrightarrow-3\le q^2\le3\Leftrightarrow-1\le q\le1\)
\(\forall q=0\Leftrightarrow k^2=\dfrac{28}{5}\left(ktm\right)\\ \forall q=\pm1\Leftrightarrow k=\pm2\\ \Leftrightarrow\left(c;d\right)=\left(6;3\right);\left(-6;-3\right);\left(-6;3\right);\left(6;-3\right)\\ \Leftrightarrow\left(a;b\right)=\left(18;9\right)\left(-18;-9\right);\left(-18;9\right);\left(18;-9\right)\\ \Leftrightarrow\left(x;y\right)=\left(54;27\right);\left(-54;-27\right);\left(54;-27\right);\left(-54;27\right)\)

Gọi nghiệm nguyên của P(x) là: k
ta có: ak3+bk2+ck+d=0ak3+bk2+ck+d=0
k.(ak2+bk+k)=−dk.(ak2+bk+k)=−d( *)
ta có: P(1)=a+b+c+dP(1)=a+b+c+d
P(0)=dP(0)=d
mà P(1); P(0) là các số lẻ
=> a+b+c+d và d là các số lẻ
mà d là số lẻ
=> a+b+c là số chẵn
Từ (*) => k thuộc Ư(d)
mà d là số lẻ
=> k là số lẻ
=> k3−1;k2−1;k−1k3−1;k2−1;k−1là các số chẵn
⇒a(k3−1)+b(k2−1)+c(k−1)⇒a(k3−1)+b(k2−1)+c(k−1) là số chẵn
=(ak3+bk2+ck)−(a+b+c)=(ak3+bk2+ck)−(a+b+c)
mà a+b+c là số chẵn
⇒ak3+bk2+c⇒ak3+bk2+c là số chẵn
Từ (*) => d là số chẵn ( vì d là số lẻ)
=> P(x) không thể có nghiệm nguyên
Xét đa thức P(x)=ax3+bx2+cx+dP(x)=ax3+bx2+cx+d
⇒P(0)=d⇒P(0)=d
P(1)=ax+bx+c+dP(1)=ax+bx+c+d
Giả sử tồn tại tại số nguyên kk là nghiệm của đa thức P(x)P(x) nên P(k)=0P(k)=0
+) Với k là số chẵn
⇒P(k)−d=ak3+bk3+ck⇒P(k)-d=ak3+bk3+ck là số chẵn
Mà P(k)−d=P(k)−P(0)=−P(0)P(k)-d=P(k)-P(0)=-P(0) là số chẵn
⇒k⇒k là số chẵn (loại) (1)
+) Với k là số lẻ
⇒P(k)−P(1)=a(k3−1)+b(k2−1)+c(k−1)⇒P(k)-P(1)=a(k3-1)+b(k2-1)+c(k-1)
Vì kk là số lẻ nên k3−1;k2−1;k−1k3-1;k2-1;k-1 là các số chẵn
⇒P(k)−P(1)⇒P(k)-P(1) là số chẵn
⇒P(1)⇒P(1) là số chẵn
⇒k⇒k là số lẻ (loại) (2)
Từ (1), (2)
⇒⇒ Không tồn tại số nguyên kk sao cho P(k)=0P(k)=0
⇒P(x)⇒P(x) không thể có nghiệm là số nguyên (đpcm)
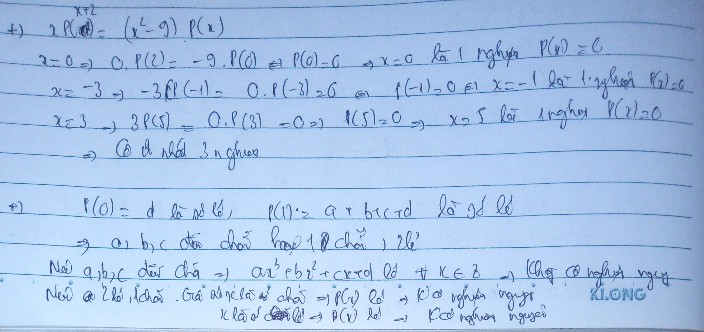
Gọi nghiệm nguyên của P(x) là: k
ta có: \(ak^3+bk^2+ck+d=0\)
\(k.\left(ak^2+bk+k\right)=-d\)( *)
ta có: \(P_{\left(1\right)}=a+b+c+d\)
\(P_{\left(0\right)}=d\)
mà P(1); P(0) là các số lẻ
=> a+b+c+d và d là các số lẻ
mà d là số lẻ
=> a+b+c là số chẵn
Từ (*) => k thuộc Ư(d)
mà d là số lẻ
=> k là số lẻ
=> \(k^3-1;k^2-1;k-1\)là các số chẵn
\(\Rightarrow a\left(k^3-1\right)+b\left(k^2-1\right)+c\left(k-1\right)\) là số chẵn
\(=\left(ak^3+bk^2+ck\right)-\left(a+b+c\right)\)
mà a+b+c là số chẵn
\(\Rightarrow ak^3+bk^2+c\) là số chẵn
Từ (*) => d là số chẵn ( vì d là số lẻ)
=> P(x) không thể có nghiệm nguyên