Cho O là trung điểm của đoạn AB. Trên cùng 1 nửa mặt phẳng có bờ là cạnh AB vẽ tia Ax, By vuông góc vs AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc vs OC cắt tia By tại D.
a) CM: \(AB^2=4AC.BD\)
b) Kẻ OM vuông góc CD tại M. CM: AC = CM
c) Từ M kẻ MH vuông góc vs AB tại H. CM: BC đi qua trung điểm MH
d) Tìm vị trí của C trên tia Ax để \(S_{ABDC}\)nhỏ nhất

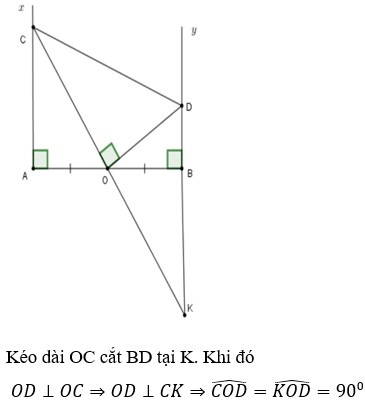





a, \(\Delta CAO~\Delta OBD\left(g-g\right)\)
\(\Rightarrow\frac{OA}{BD}=\frac{AC}{OB}\Rightarrow\frac{AB}{2BD}=\frac{2AC}{AB}\Rightarrow AB^2=4.AC.BD\)
b, \(\Delta CAO~\Delta COD\left(c-g-c\right)\Rightarrow\widehat{ACO}=\widehat{MCO}\)
\(\Delta CAO=\Delta CMO\left(ch-gn\right)\Rightarrow AC=CM\)
c, Gọi giao điểm MH và BC là N
Tương tự b, BD=MD
Do \(CA//BD\Rightarrow\frac{CA}{BD}=\frac{CN}{NB}\Rightarrow\frac{CN}{NB}=\frac{CM}{MD}\)
\(\Rightarrow MN//BD\Rightarrow NH//BD\Rightarrow\frac{NH}{BD}=\frac{NA}{BD}\Rightarrow\frac{NH}{BD}=\frac{CN}{NB}\Rightarrow\frac{NH}{BD}=\frac{NM}{BD}\)
\(\Rightarrow NM=NH\)
d, Ta có: \(S_{ABCD}=\frac{\left(CA+BD\right)AB}{2}\ge\frac{AC.BD.AB}{2}=\frac{\frac{AB^2}{4}.AB}{2}=\frac{AB^3}{8}\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}AC=BD\\AC.BD=\frac{AB^2}{4}\end{cases}\Rightarrow}AC=BD=\frac{AB}{2}\)
OK, GOOD LUCK!!!
Lần sau làm câu d thôi