Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(a)\) Ta có :
\(\frac{m-2}{4}+\frac{3m+1}{3}< 0\)
\(\Leftrightarrow\)\(\frac{3m-6+12m+4}{12}< 0\) ( quy đồng )
\(\Leftrightarrow\)\(3m-6+12m+4< 0\)
\(\Leftrightarrow\)\(\left(12m+3m\right)+\left(4-6\right)< 0\)
\(\Leftrightarrow\)\(15m-2< 0\)
\(\Leftrightarrow\)\(15m< 2\)
\(\Leftrightarrow\)\(m< \frac{2}{15}\)
Vậy để \(\frac{m-2}{4}+\frac{3m+1}{3}\) có giá trị âm thì \(m< \frac{2}{15}\)
Chúc bạn học tốt ~
\(b)\) Ta có :
\(\frac{m-4}{6m+9}>0\)
\(\Leftrightarrow\)\(m-4>0\) ( nhân hai vế cho \(6m+9\) )
\(\Leftrightarrow\)\(m>4\)
Vậy để \(\frac{m-4}{6m+9}\) có giá trị dương thì \(m>4\)
Chúc bạn học tốt ~
a) \(x-3=2m+4\)
\(\Leftrightarrow x=2m+4+3\)
\(\Leftrightarrow x=2m+7\)
Phương trình có nghiệm dương khi \(2m+7>0\Leftrightarrow m>-\dfrac{7}{2}\)
b) \(2x-5=m+8\)
\(\Leftrightarrow2x=m+8+5\)
\(\Leftrightarrow2x=m+13\)
\(\Leftrightarrow x=\dfrac{m+13}{2}\)
Phương trình có nghiệm âm khi: \(\dfrac{m+13}{2}< 0\Leftrightarrow m< -13\)
c) \(x-2=3m+4\)
\(\Leftrightarrow x=3m+4+2\)
\(\Leftrightarrow x=3m+6\)
Phương trình có nghiệm lớn hơn 3 khi: \(3m+6>3\Leftrightarrow m>-1\)
Quy đồng :
\(A=\frac{2m-3}{2m+3}+\frac{2m+3}{2m-3}\)Đ k : \(\hept{\begin{cases}m\ne\frac{-3}{2}\\m\ne\frac{3}{2}\end{cases}}\)
\(=\frac{\left(2m-3\right)^2+\left(2m+3\right)^2}{\left(2m+3\right)\left(2m-3\right)}\)
\(=\frac{\left(2m-3\right)^2+\left(2m+3\right)^2}{4m^2-9}=P\)
Để A có giá trị âm thì : \(4m^2-9< 0\Rightarrow\left(2m-3\right)\left(2m+3\right)< 0\)
Th1 : \(\hept{\begin{cases}2m-3< 0\\2m+3>0\end{cases}}\Rightarrow\hept{\begin{cases}m< \frac{3}{2}\\m>\frac{-3}{2}\end{cases}}\)
Th2 : \(\hept{\begin{cases}2m-3>0\\2m+3< 0\end{cases}\Rightarrow\hept{\begin{cases}m>\frac{3}{2}\\m< \frac{-3}{2}\end{cases}}}\)
Này bạn, các trường hợp như vậy thì phải dùng dấu \(\Leftrightarrow\)nha bạn không là sai
Chọn đáp án C.
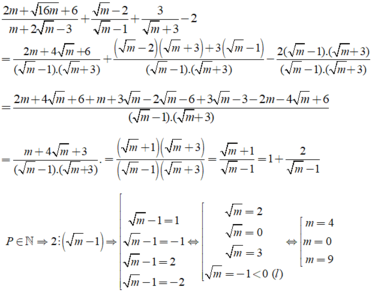
Thử lại, với m= 4 thì P =3 ( thỏa mãn)
Với m = 0 thì P = -1 ( không là số tự nhiên).
Với m = 9 thì P = 2 ( thỏa mãn)
Vậy m = 4 hoặc m = 9.
Thay x=1 và A=0 vào biểu thức, ta được:
\(\dfrac{3}{2m+1}+\dfrac{5}{2m-1}=0\)
=>6m-3+10m+5=0
=>16m+2=0
hay m=-1/8
\(\frac{-m+1}{m+8}+\frac{m-1}{m+3}\)( ĐKXĐ : \(x\ne-8;x\ne-3\))
\(=\frac{\left(-m+1\right)\left(m+3\right)}{\left(m+8\right)\left(m+3\right)}+\frac{\left(m-1\right)\left(m+8\right)}{\left(m+8\right)\left(m+3\right)}\)
\(=\frac{-m^2-2m+3}{\left(m+8\right)\left(m+3\right)}+\frac{m^2+7m-8}{\left(m+8\right)\left(m+3\right)}\)
\(=\frac{-m^2-2m+3+m^2+7m-8}{\left(m+8\right)\left(m+3\right)}\)
\(=\frac{5m-5}{\left(m+8\right)\left(m+3\right)}\)
Để biểu thức dương ( tức > 0 ) ta xét hai trường hợp sau :
I) \(\hept{\begin{cases}5m-5>0\\\left(m+8\right)\left(m+3\right)>0\end{cases}}\)
+) 5m - 5 > 0 => 5m > 5 => m > 1 (1)
+) ( m + 8 )( m + 3 ) > 0
1. \(\hept{\begin{cases}m+8>0\\m+3>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-8\\m>-3\end{cases}}\Leftrightarrow m>-3\)(2)
2. \(\hept{\begin{cases}m+8< 0\\m+3< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -8\\m< -3\end{cases}}\Leftrightarrow m< -8\)(3)
Từ (1) , (2) và (3) => m > 1
II) \(\hept{\begin{cases}5m-5< 0\\\left(m+8\right)\left(m+3\right)< 0\end{cases}}\)
+) 5m - 5 < 0 => 5m < 5 => m < 1 (4)
+) ( m + 8 )( m + 3 ) < 0
1. \(\hept{\begin{cases}m+8< 0\\m+3>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -8\\m>-3\end{cases}}\)( loại )
2. \(\hept{\begin{cases}m+8>0\\m+3< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-8\\m< -3\end{cases}}\Leftrightarrow-8< m< -3\)(5)
Từ (4) và (5) => -8 < m < -3
Từ I) và 2)
=> Với m > 1 hoặc -8 < m < -3 thì biểu thức có giá trị dương
\(\frac{\left(m+1\right)\left(m-5\right)}{2}\)có giá trị âm
=> ( m + 1 )( m - 5 ) < 0
Xét hai trường hợp :
1. \(\hept{\begin{cases}m+1< 0\\m-5>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -1\\m>5\end{cases}}\)( loại )
2. \(\hept{\begin{cases}m+1>0\\m-5< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-1\\m< 5\end{cases}}\Leftrightarrow-1< m< 5\)
Vậy với -1 < m < 5 thì biểu thức có giá trị âm
Bài làm:
a) Ta có: \(\frac{-m+1}{m+8}+\frac{m-1}{m+3}\) \(\left(m\ne\left\{-8;-3\right\}\right)\)
\(=\frac{\left(1-m\right)\left(m+3\right)+\left(m-1\right)\left(m+8\right)}{\left(m+8\right)\left(m+3\right)}\)
\(=\frac{\left(m-1\right)\left(m+8-m-3\right)}{\left(m+8\right)\left(m+3\right)}\)
\(=\frac{5\left(m-1\right)}{\left(m+8\right)\left(m+3\right)}\)
Để BT có giá trị dương thì ta xét 2 TH sau:
+ Nếu: \(\hept{\begin{cases}5\left(m-1\right)>0\\\left(m+8\right)\left(m+3\right)>0\end{cases}}\Rightarrow m>1\)
+ Nếu: \(\hept{\begin{cases}5\left(m-1\right)< 0\\\left(m+8\right)\left(m+3\right)< 0\end{cases}}\Rightarrow-8< m< -3\)
a) Bpt <=> \(\frac{m-2}{4}+\frac{3m+1}{3}< 0\)
\(\Leftrightarrow3\left(m-2\right)+4\left(3m+1\right)< 0\)
\(\Leftrightarrow3m-6+12m+4< 0\)
\(\Leftrightarrow3m+12m-2< 0\)
\(\Leftrightarrow15m-2< 0\)
\(\Leftrightarrow15m< 2\)
\(\Leftrightarrow m< \frac{2}{15}\)
Vậy để bt đạt giá trị âm thì m < 2/15
làm hộ mink câu cuối đi