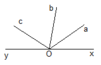
Cho góc bẹt xoy . Trên cùng một nửa mặt phẳng bờ xy vẽ các tia oc,od sao cho xoc = yod . kể tên các tia phân giác của 2 góc có trong hình\
Help me ? Bài khó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 12 2017
Có 10 góc, đó là các góc x O a , x O b , x O c , x O y , a O b , a O c , a O y , b O c , b O y , c O y
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
15 tháng 7 2021
a) Ta có: \(\widehat{BOC}+\widehat{COA}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{BOC}+60^0=180^0\)
hay \(\widehat{BOC}=120^0\)
\(\Leftrightarrow2\cdot\widehat{xOB}=120^0\)
hay \(\widehat{xOB}=60^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OB, ta có: \(\widehat{xOB}< \widehat{BOD}\left(60^0< 90^0\right)\)
nên tia Ox nằm giữa hai tia OB và OD
\(\Leftrightarrow\widehat{BOx}+\widehat{xOD}=\widehat{BOD}\)
\(\Leftrightarrow\widehat{xOD}+60^0=90^0\)
hay \(\widehat{xOD}=30^0\)
b) Ta có: \(\widehat{AOC}+\widehat{COD}=90^0\)
nên \(\widehat{COD}=30^0\)
Ta có: tia OD nằm giữa hai tia OC và Ox
mà \(\widehat{xOD}=\widehat{COD}\left(=30^0\right)\)
nên OD là tia phân giác của \(\widehat{xOC}\)
