Cho phương trình (m2 – 4)x + 2 = m
Giải phương trình trong mỗi trường hợp sau:
a. m = 2
b. m = - 2
c. m = - 2,2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
25 tháng 10 2018
Khi m = -2,2, phương trình đã cho trở thành:
[ - 2 , 2 2 – 4]x + 2 = -2,2 ⇔ 0,84x + 2 = -2,2
⇔ 0,84x = -2,2 – 2 ⇔ 0,84x = -4,2 ⇔ x = -5
Vậy phương trình đã cho có nghiệm x = -5.
TN
22 tháng 5 2016
a)với m=2 ta có:
(22-4)x+2=2
<=>0*x+2=2
<=>0x=0
<=>x có thể nhận tất cả giá trị
b)với m=-2 ta có:
[(-2)2-4)x+2=2
tương tự như phần a
c)với m=-2,2 ta có:
[(-2,2)2-4]x+2=-2,2
<=>4,84*x+2=-2,2
<=>4,84*x=-4,2
<=>x=.. tự tính
22 tháng 5 2016
a)với m=2 ta có:
(22-4)x+2=2
<=>0*x+2=2
<=>0x=0
<=>x có thể nhận tất cả giá trị
b)với m=-2 ta có:
[(-2)2-4)x+2=2
tương tự như phần a
c)với m=-2,2 ta có:
[(-2,2)2-4]x+2=-2,2
<=>4,84*x+2=-2,2
<=>4,84*x=-4,2
<=>x=.. tự tính
Ai k mk mk k lại
0
26 tháng 3 2018
Giải:
a. Khi m = 2, phương trình đã cho trở thành:
(22−4)x+2=2⇔0x+2=2⇔2=2(22−4)x+2=2⇔0x+2=2⇔2=2
Vậy phương trình đã cho có vô số nghiệm.
b. Khi m = -2, phương trình đã cho trở thành:
[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4
Vậy phương trình đã cho vô nghiệm.
c. Khi m = -2,2, phương trình đã cho trở thành:
[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5
Vậy phương trình đã cho có nghiệm x = -5
AH
Akai Haruma
Giáo viên
6 tháng 1 2023
Bài 9:
Không, vì $x+2=0$ có nghiệm duy nhất $x=-2$ còn $\frac{x}{x+2}=0$ ngay từ đầu đkxđ đã là $x\neq -2$ (cả 2 pt không có cùng tập nghiệm)
AH
Akai Haruma
Giáo viên
6 tháng 1 2023
Bài 8:
a. Khi $m=2$ thì pt trở thành:
$(2^2-9)x-3=2$
$\Leftrightarrow -5x-3=2$
$\Leftrightarrow -5x=5$
$\Leftrightarrow x=-1$
b.
Khi $m=3$ thì pt trở thành:
$(3^2-9)x-3=3$
$\Leftrightarrow 0x-3=3$
$\Leftrightarrow 0=6$ (vô lý)
c. Khi $m=3$ thì pt trở thành:
$[(-3)^2-9]x-3=-3$
$\Leftrightarrow 0x-3=-3$ (luôn đúng với mọi $x\in\mathbb{R}$)
Vậy pt vô số nghiệm thực.
CM
28 tháng 8 2018
Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: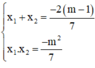 
Khi đó:
TA
25 tháng 5 2021
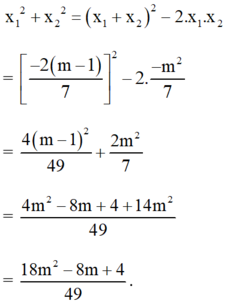
Viet: `x_1+x_2=2m+2`
`x_1x_2=m^2+m-1`
Có: `1/(x_1^2)+1/(x_2^2)`
`=(x_1^2+x_2^2)/(x_1^2 x_2^2)`
`=( (x_1+x_2)^2-2x_1x_2)/(x_1^2 x_2^2)`
`=((2m+2)^2-2(m^2+m-1))/((m^2+m-1)^2)`
`=(2m^2+6m+6)/(m^4+2m^3−m^2−2m+1)`
CM
12 tháng 7 2019
Giả sử phương trình đã cho có 2 nghiệm x 1 và x 2 , theo hệ thức Vi-ét ta có:
x 1 + x 2 = -b/a = -[-2(m + 1)]/1 = 2(m + 1)/1 = 2(m + 1)
x 1 x 2 = c/a = ( m 2 + m - 1)/1 = m 2 + m – 1
x 1 2 + x 2 2 = x 1 + x 2 2 – 2 x 1 x 2 = 2 m + 2 2 – 2( m 2 + m – 1)
= 4 m 2 + 8m + 4 – 2 m 2 – 2m + 2 = 2 m 2 + 6m + 6
CM
16 tháng 1 2017
a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: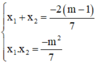 
Khi đó:
PT
1
CM
29 tháng 9 2017
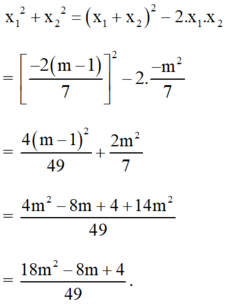
Khi m = -2, phương trình đac cho trở thành:
[ - 2 2 – 4]x + 2 = -2 ⇔ 0x + 2 = -2 ⇔ 0x = -4
Vậy phương trình đã cho vô nghiệm.
Giải:
a. Khi m = 2, phương trình đã cho trở thành:
(22−4)x+2=2⇔0x+2=2⇔2=2(22−4)x+2=2⇔0x+2=2⇔2=2
Vậy phương trình đã cho có vô số nghiệm.
b. Khi m = -2, phương trình đã cho trở thành:
[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4[(−2)2−4]x+2=−2⇔0x+2=−2⇔0x=−4
Vậy phương trình đã cho vô nghiệm.
c. Khi m = -2,2, phương trình đã cho trở thành:
[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5[(−2,2)2−4]x+2=−2,2⇔0,84x+2=−2,2⇔0,84x=−2,2−2⇔0,84x=−4,2⇔x=−5
Vậy phương trình đã cho có nghiệm x = -5
mấy bài giải phương trình kiểu vầy ko ai giỏi hơn casio và vinacal đâu. hé hé :)))