Cho mk một số bài toán khó về chứng minh bất đẳng thức và tìm GTLN, GTNN với. Nhớ ghi thêm cách giải sơ lược nha.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vd : \(x^2+6x+10\)
Ta có : 10 không căn được
Mà : \(x^2+2.x.3+3^2\)
Nhưng 32 chỉ là 9 nên ta cộng thêm 1 ở vế sau
\(\left(x^2+2.x.3+3^2\right)+1\)
\(\left(x+3\right)^2+1\)
Dư 1 ở ngoài :
Vì \(\left(x+3\right)^2\ge0\)
=> \(\left(x+3\right)^2+1\ge1\)
=> GTNN là 1
Khi ( x + 3 ) = 0
x = -3
Khi
Giải
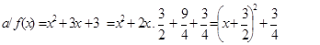
Ta có 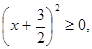 nên
nên 
Vậy: f(x) đạt GTNN bằng  khi
khi 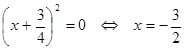
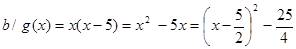
Ta có  nên
nên 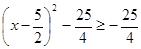
Vậy: g(x) đạt GTNN bằng  khi
khi 

một bài bđt khó nha cho a,b,c là các số dương thỏa mãn a+b+c=3. Tìm giá trị nhỏ nhất của biểu thức sau:
P=1/1+a^2 +1/1+b^2 +1/1+c^2

a)Có \(a^2+1\ge2a\) với mọi a; \(b^2+1\ge2b\) với mọi b
Cộng vế với vế \(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\)
Dấu = xảy ra <=> a=b=1
b) Áp dụng BĐT bunhiacopxki có:
\(\left(x+y\right)^2\le\left(1+1\right)\left(x^2+y^2\right)\Leftrightarrow\left(x+y\right)^2\le2\)
\(\Leftrightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(\Rightarrow\left(x+y\right)_{max}=\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=\dfrac{\sqrt{2}}{2}\)
\(\left(x+y\right)_{min}=-\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=-\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=-\dfrac{\sqrt{2}}{2}\)
c) \(S=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}=\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}+\dfrac{1}{2ab}\)
Với x,y>0, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) (1)
Thật vậy (1) \(\Leftrightarrow\dfrac{y+x}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)\(\Leftrightarrow\left(x-y\right)^2\ge0\) (lđ)
Áp dụng (1) vào S ta được:
\(S\ge\dfrac{4}{a^2+b^2+2ab}+\dfrac{1}{2ab}\)
Lại có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\) \(\Leftrightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow2ab\le\dfrac{1}{2}\)\(\Rightarrow\dfrac{1}{2ab}\ge2\)
\(\Rightarrow S\ge\dfrac{4}{\left(a+b\right)^2}+2=6\)
\(\Rightarrow S_{min}=6\Leftrightarrow a=b=\dfrac{1}{2}\)


Số lớn nhất có 3 CS lẻ chia hết cho 5 là: 995
Số nhỏ nhất có 3 CS lẻ chia hết cho 5 là : 105
Dãy số có khoảng cách là 10
Vậy có : ( 995-105):10+1=90 ( số)
DE OM . EM HOC LOP 4 CHI HOC LOP 5 NEN BAI TOAN NAY DOI VOI CHI AL QUA DE EM A


1) \(\left(a+b\right)^2\left(b+c\right)^2\ge4abc\left(a+b+c\right)\)
2) Cho \(a+b=2.\)CMR:
a) \(a^2+b^2\ge2\)
b) \(a^4+b^4\ge2\)
c) \(a^8+b^8\ge2\)
3) \(a+b+c+d=2.\) CMR \(a^2+b^2+c^2+d^2\ge1\)