Cho hình vuông ABCD. Gọi M và N là trung điểm của BC và DC. Tính cos góc MAN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BM
1
5 tháng 10 2020
Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)
NL
0
PT
1
CM
17 tháng 10 2018
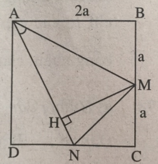
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
NT
0
CM
21 tháng 3 2019
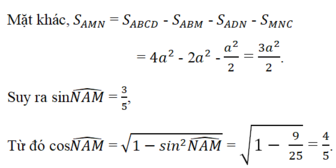
Chọn A.
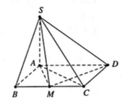
Gắn tọa độ Oxyz, với A(0;0;0), B(1;0;0), D(0;3;0), S(0;0;1)
Khi đó C ( 1 ; 3 ; 0 ) ⇒ Trung điểm M của BC là M ( 1 ; 3 2 ; 0 ) .
Ta có
SM → = ( 1 ; 3 2 ; - 1 ) , SD → = ( 0 ; 3 ; - 1 ) ⇒ [ SM → ; SD → ] = ( 3 2 ; 1 ; 3 ) .
Suy ra n ⃗ ( SDM ) = ( 3 2 ; 1 ; 3 ) mà n ⃗ ( ABCD ) = n ⃗ ( Oxy ) = ( 0 ; 0 ; 1 ) ,
ta được
cos ( SDM ^ ) ; ( ABCD ) = n → ( SDM ) . n → ( ABCD ) n → ( SDM ) . n → ( ABCD ) = 6 7 .
cos(300) =\(\frac{\sqrt{3}}{2}\)
lik-e nha