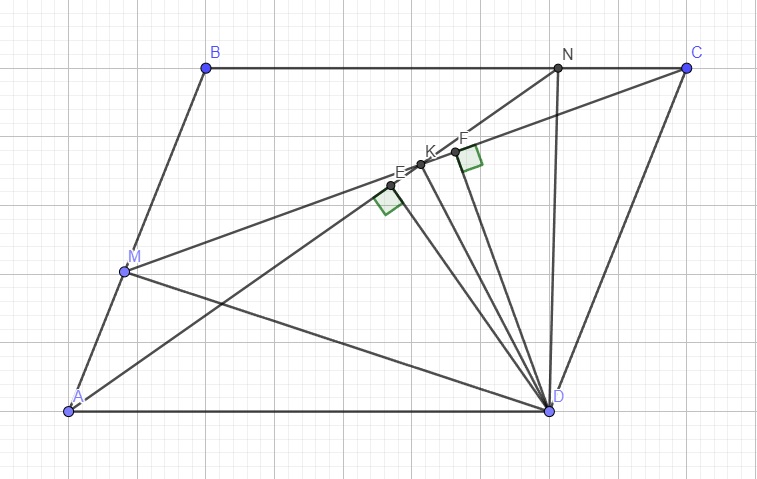
cho hình bình hành ABCD , các điểm M, N theo thứ tự thuộc các cạnh AB, BC sao cho AN=CM , gọi K là giao điểm của AN và CM . chúng minh rằng KD là tia phân giác cảu góc AKD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Trước hết ta chứng minh bổ đề sau (nếu em chưa học)
Cho 4 điểm A; B; C; D phân biệt sao cho \(AB||CD\), khi đó ta luôn có: \(S_{\Delta ACD}=S_{\Delta BCD}\)
C/m: từ A và B lần lượt kẻ \(AH\) và \(BK\) vuông góc CD \(\Rightarrow AH||BK\Rightarrow\) tứ giác AHKB là hình chữ nhật
\(\Rightarrow AH=BK\)
Do \(\left\{{}\begin{matrix}S_{\Delta ACD}=\dfrac{1}{2}AH.CD\\S_{\Delta BCD}=\dfrac{1}{2}BK.CD\end{matrix}\right.\) mà \(AH=BK\Rightarrow S_{\Delta ACD}=S_{\Delta BCD}\) (đpcm)
Quay lại bài toán, áp dụng bổ đề trên ta có: do N thuộc BC nên \(NC||AD\Rightarrow S_{\Delta NAD}=S_{\Delta CAD}\) (1)
Tương tự, \(AM||CD\Rightarrow S_{\Delta ACD}=S_{\Delta MCD}\) (2)
(1);(2) \(\Rightarrow S_{\Delta NAD}=S_{\Delta MCD}\)
Từ D lần lượt kẻ \(DE\perp AN\) và \(DF\perp CM\)
\(\Rightarrow\left\{{}\begin{matrix}S_{\Delta NAD}=\dfrac{1}{2}DE.AN\\S_{\Delta MCD}=\dfrac{1}{2}DF.CM\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}S_{\Delta NAD}=S_{\Delta MCD}\\AN=CM\end{matrix}\right.\) \(\Rightarrow DE=DF\)
\(\Rightarrow\Delta_VDEK=\Delta_VDFK\left(ch-cgv\right)\)
\(\Rightarrow\widehat{EKD}=\widehat{FKD}\) hay KD là phân giác
11 tháng 2 2020
Cảm ơn bạn vì đã có ý giúp nhưng mình tìm được câu tương tự rồi. Cảm ơn bạn nhiều
