Cho đường tròn tâm O và dây AB, điểm M di động trên đường tròn. Gọi H là chân đường vuông góc kẻ từ M tới AB. Gọi E, F lần lượt là hình chiếu vuông góc của H trên MA, MB. Qua M kẻ đường thẳng vuông góc với EF cắt AB tại D. a) Chứng minh đường thẳng MD luôn đi qua một điểm cố định khi M thay đổi trên đường tròn.b)...
Đọc tiếp
Cho đường tròn tâm O và dây AB, điểm M di động trên đường tròn. Gọi H là chân đường vuông góc kẻ từ M tới AB. Gọi E, F lần lượt là hình chiếu vuông góc của H trên MA, MB. Qua M kẻ đường thẳng vuông góc với EF cắt AB tại D.
a) Chứng minh đường thẳng MD luôn đi qua một điểm cố định khi M thay đổi trên đường tròn.
b) CMR: \(\frac{MA^2}{MB^2}=\frac{AH.AD}{BH.BD}\)
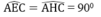
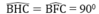
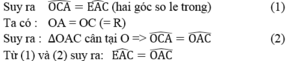
a)
Từ M kẻ tiếp tuyến Mx của (O) nên OA vuông góc với Mx
Ta có tứ giác MEHF là tứ giác nội tiếp => góc MFE=góc MHE(1)
Mà góc MHE=góc MAH(2) (+góc HMA=90o)
Từ (1) và (2) => góc MAB = góc MFE
Mặt khác góc MAB=góc BMx (=1/2 số đo cung MB )
=>EF song song với Mx
Om vuông góc Mx => OM vuông góc È
mà MD vuông góc È => o thuộc MD => dpcm
làm câu b đi bạn