cho a,b,c là các số dương đôi một khác nhau có tổng là 12.CMR trong ba phương trình sau có một phương trình vô nghiệm 1 phương trình có nghiệm
(1) x2+ax+b=0
(2)x2+bx+c=0
(3)x2+cx+a=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2020
Ta có:
\(\Delta_1+\Delta_2+\Delta_3=a^2-4b+b^2-4c+c^2-4a=a^2+b^2+c^2-48\)
Dễ thấy:\(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=48\Rightarrow\Delta_1+\Delta_2+\Delta_3\ge0\)
Khi đó có ít nhất một phương trình có nghiệm
17 tháng 11 2017
Các giải của các bài toán này là sử dụng tổng các delta em nhé
17 tháng 6 2016
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
CM
19 tháng 1 2019
c và d là nghiệm của phương trình:
x 2 + a x + b ⇒ ⇒ c + d = − a ( 1 ) c d = b ( 2 )
a, b là nghiệm của phương trình:
x 2 + c x + d = 0 ⇒ ⇒ a + b = − c ( 3 ) a b = d ( 4 )
Đáp án cần chọn là: A
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Câu 3:
$\Delta=2015^2-4.2013.2=2011^2$
Do đó pt có 2 nghiệm:
$x_1=\frac{2015+2011}{2.2013}=1$
$x_2=\frac{2015-2011}{2.2013}=\frac{2}{2013}$
Đáp án B.
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Câu 4:
Theo định lý Viet, tổng các nghiệm của pt là:
$S=\frac{-b}{a}=\frac{-3}{1}=-3$
Đáp án B.
9 tháng 7 2019
Câu hỏi của Trần Hà My - Toán lớp 9 - Học toán với OnlineMath
Bạn tham khảo link này nhé!
CM
8 tháng 5 2017
Không gian mẫu khi gieo con súc sắc cân đối và đồng chất:
Ω = {1, 2, 3, 4, 5, 6}
⇒ n(Ω) = 6
Đặt A: "con súc sắc xuất hiện mặt b chấm";
Xét : x2 + bx + 2 = 0 (1)
Δ = b2 – 8
a. Phương trình (1) có nghiệm
⇔ Δ ≥ 0 ⇔ b ≥ 2√2
⇒ b ∈ {3; 4; 5; 6}.
⇒ A = {3, 4, 5, 6}
⇒ n(A) = 4
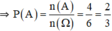
b. (1) vô nghiệm
⇔ Δ < 0 ⇔ b ≤ 2√2
⇒ b ∈ {1; 2}
⇒ A = {1, 2}
⇒ n(A) = 2
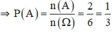
c. phương trình (1) có nghiệm
⇔ b ∈ {3; 4; 5; 6}.
Thử các giá trị của b ta thấy chỉ có b = 3 phương trình cho nghiệm nguyên.
⇒ A = {3}
⇒ n(A) = 1
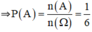
bt đc chết liền