CHO TỨ GIÁC ABCD CÓ GÓC DAC =GÓC DBC CMR
AB.DC+AD.BC=AC.BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
1
15 tháng 2 2023
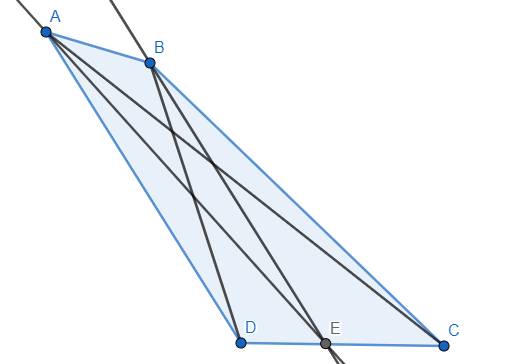
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)
Ta có hình vẽ:
Ta có: \(\widehat{dAc}=\widehat{dBc}\)
\(AB.DC=AD.BC=AC.BD\Leftrightarrow\frac{AB}{AD}+\frac{CB}{CD}=\frac{AB}{CD}\)
Mà \(\widehat{dAc}\infty\widehat{dBc}\) (c.g.c)
Từ đó, suy ra \(AB.DC+AD.BC=AC.BD\) (g.g)
Suy ra ĐPCM
P/s: Mình không chắc. sai thì thôi nha!