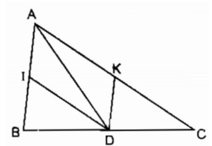
Cho tam giác ABC cân ở A có AI là phân giác và CH là đường cao.
a. Tính BH nếu biết AB=10cm, BC=6cm.
b. Đường thẳng qua I song song với AB cắt AC ở K. Đường thẳng qua K song song với BC cắt AB ở J. Chứng minh HIKJ là hình thang cân.
c. Chứng minh BH.CK=BI^2 và tam giác BIH đồng dạng với tam giác IKH
d. Chứng minh IK.HB+KC.IH > HK.BI
e. Gọi O là giao điểm của IJ và HK, AO cắt BC ở E. Dựng góc BCx kề góc BCA sao cho góc BCx bằng góc BAE. Hai tia AE và Cx cắt nhau ở D. Chứng minh tam giác BED đồng dạng với tam giác AEC và AC^2 = AD.AE
g. Chứng minh AD^2=BD.CD + AB^2