16x2+22x-3=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
W
1
11 tháng 7 2021
a) Ta có: \(a^3\)
\(=\left(\sqrt{5}+\sqrt{3}\right)^3\)
\(=5\sqrt{5}+15\sqrt{3}+9\sqrt{5}+3\sqrt{3}\)
b) Ta có: \(a^4-16a^2+4=0\)
\(\Leftrightarrow\left(\sqrt{5}+\sqrt{3}\right)^4-16\left(\sqrt{5}+\sqrt{3}\right)^2+4=0\)
\(\Leftrightarrow\left(8+2\sqrt{15}\right)^2-16\left(8+2\sqrt{15}\right)+4=0\)
\(\Leftrightarrow64+32\sqrt{15}+60-128-32\sqrt{15}+4=0\)
\(\Leftrightarrow0=0\)(đúng)
4 tháng 10 2021
\(7x\left(16x^2-1\right)=0\)
\(\Leftrightarrow7x\left(4x-1\right)\left(4x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
TG
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
b.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\sqrt{2}\left(sinx+cosx\right)=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}\)
\(\Leftrightarrow\sqrt{2}\left(sinx+cosx\right)=\dfrac{1}{sinx.cosx}\)
Đặt \(sinx+cosx=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(sinx.cosx=\dfrac{t^2-1}{2}\)
Pt trở thành:
\(\sqrt{2}t=\dfrac{2}{t^2-1}\Rightarrow t^3-t-\sqrt{2}=0\)
\(\Leftrightarrow\left(t-\sqrt{2}\right)\left(t^2+\sqrt{2}t+1\right)=0\)
\(\Leftrightarrow t=\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow x+\dfrac{\pi}{4}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k2\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
a.
\(\Leftrightarrow sin^22x+cos^22x+\sqrt{3}sin4x+1+cos4x=0\)
\(\Leftrightarrow cos4x+\sqrt{3}sin4x=-2\)
\(\Leftrightarrow\dfrac{1}{2}cos4x+\dfrac{\sqrt{3}}{2}sin4x=-1\)
\(\Leftrightarrow cos\left(4x-\dfrac{\pi}{3}\right)=-1\)
\(\Leftrightarrow4x-\dfrac{\pi}{3}=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k\pi}{2}\)
CM
4 tháng 6 2019
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính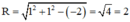 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
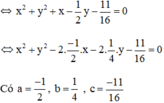
⇒ Đường tròn có tâm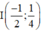 
, bán kính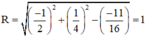 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính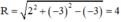 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
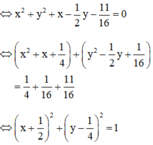
Vậy đường tròn có tâm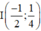 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
11 tháng 1 2023
=>2x(x^2-11x+18)=0
=>x(x-2)(x-9)=0
=>\(x\in\left\{0;2;9\right\}\)
14 tháng 10 2021
\(a,\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ b,\Leftrightarrow\left(3x-5\right)^2=0\Leftrightarrow x=\dfrac{5}{3}\)
18 tháng 11 2021
\(a,\Leftrightarrow x-28=-45\\ \Leftrightarrow x=-27\\ b,\Leftrightarrow3+x=0\\ \Leftrightarrow x=-3\\ c,\Leftrightarrow\left[{}\begin{matrix}7-x=0\\-x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ d,\Leftrightarrow16\left(x^2-4\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
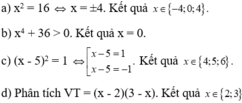
pt <=> (16x^2-24x)+(2x-3) = 0
<=> (2x-3).(8x+1) = 0
<=> 2x-3=0 hoặc 8x+1=0
<=> x=3/2 hoặc x=-1/8
Vậy ..............
Theo bài ra ta có:\(16.x^2+22x-3=0\)
\(\Rightarrow\left(16x+22\right)x=3=1.3=3.1=\left(-1\right).\left(-3\right)=\left(-3\right).\left(-1\right)\)
Tự kẻ bẳng nha