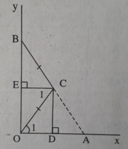
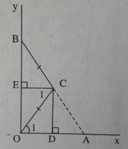
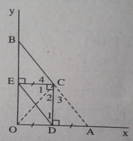
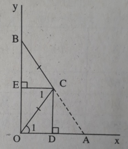
Cho \(\widehat{xoy}\) khác góc bẹt, lấy điểm A thuộc Ox, B thuộc Oy/ OA=OB. Đường vuông góc với OA tại A là đường vuông góc với OB tại B cắt nhau ở C. BC cắt Ox ở D, AC cắt Oy ở E. CMR :
a) OC à phân giác của \(\widehat{xoy}\)
b) Tam giác ODE là tam giác cân
c) OC vuông góc với DE