Cho tam giác ABC. CMR nếu trong tam giác có điểm D sao cho AD=AB thì AB<AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 1 2019
1.
Chọn điểm D như hình vẽ. Gọi E là giao điểm của AB và DC.
Ta có: \(\widehat{ADE}\)là góc ngoài của tam giác ADC => \(\widehat{ADE}>\widehat{ACD}\)(1)
Tương tự \(\widehat{BDE}>\widehat{BCD}\)(2)
(1), (2) => \(\widehat{ADB}>\widehat{ACB}\)
Mà \(\widehat{ADB}=\widehat{ABD}\)
=> \(\widehat{ABC}>\widehat{ABD}=\widehat{ADB}>\widehat{ACB}\)
=> AC>AB
T
27 tháng 1 2019
Xét tam giác ABC vuông tại A
Theo BĐT tam giác: \(AB< AC+BC\)
Và tam giác AHC vuông tại H có: \(AC< AH+CH\) (1)
\(\Rightarrow AB+AC< \left(AH+BC\right)+\left(AC+CH\right)\)
Hay \(AB+AC< \left(AH+CH+BH\right)+\left(AC+CH\right)\)
Hay \(AB+AC< AH+2CH+BH+AC\)
Bớt AC ở cả hai vế: \(AB< AH+2CH+BH\) (2)
Từ (1) và (2) suy ra \(AB+AC< 2AH+2CH+BH+CH\)
Hay \(AB+AC< 2AH+2CH+BC\)
Tới đây bí rồi.
LD
0
5 tháng 1 2022
hình tự vẽ
a)Vì AD là tpg của ^BAC
=>^BAD = ^CAD = ^BAC/2
Xét tam giác ABD và tam giác AED có:
AD:cạnh chung
^BAD=^CAD(cmt)
AB=AE(gt)
=>tam giác ABD=tam giác AED (c.g.c)
=>BD=BE (cặp cạnh t.ư)
b)Vì tam giác ABD=tam giác AED(cmt)
=>^ABD=^AED (cặp góc t.ư)
Ta có:^ABD+^KBD=1800 (kề bù)
=>^KBD=1800-^ABD (1)
^AED+^CED=1800 (kề bù)
=>^CED=1800-^AED(2)
Từ (1);(2);có ^ABD=^AED(cmt)
=>^KBD=^CED
Xét tam giác DBK và tam giác DEC có:
BD=BE(cmt
^KBD=^CED(cmt)
^BDK=^EDC (2 góc đđ)
=>tam giác DBK=tam giác DEC (g.c.g)
5 tháng 1 2022
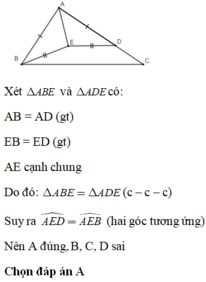
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: BD=ED
b: Xét ΔDBK và ΔDEC có
\(\widehat{DBK}=\widehat{DEC}\)
BD=ED
\(\widehat{BDK}=\widehat{EDC}\)
Do đó: ΔDBK=ΔDEC
c: Ta có: ΔDBK=ΔDEC
nên BK=EC
Ta có: AB+BK=AK
AE+EC=AC
mà AB=AE
và BK=EC
nên AK=AC
hay ΔAKC cân tại A
4 tháng 5 2016
a)Xét tam giác ABD và tam giác AED
AB=AE(Gt)
BAD=DAE(vì AD là tia p/giác)
AD là cạnh chung)
\(\Rightarrow\) tam giác ABD=tam giác AED(c.g.c)
b)Xét tam giác ADF và tam giác ADC
AF+AC(Gt)
BAD=DAE(vì AD là tia p/giác)
AD là cạnh chung
\(\Rightarrow\)tam giác ADF=tam giác ADC(c.g.c)
\(\Rightarrow\)DF=DC(cặp cạnh tương ứng)
c)Xét tam giác AMF và tam giác AMC
AF+AC(Gt)
BAD=DAE(vì AD là tia p/giác)
AD là cạnh chung
\(\Rightarrow\)tam giác AMF=tam giác AMC(c.g.c)
\(\Rightarrow\)AMF=AMC(cặp góc tương ứng)
Mà AMF+AMC=1800(kề bù)
\(\Rightarrow\)AMF=AMC=1800:2=900
Do đó Am vuông góc với CF
5 tháng 5 2016
a)XÉT ▲ABD VÀ ▲AED CÓ:
AD CHUNG
AB=AE(GT)
GÓC BAD= GÓC EAD (AD LÀ PHÂN GIÁC)
=> ▲ABD= ▲AED(C-G-C)
18 tháng 12 2022
Xét ΔABH và ΔADH có
AB=AD
góc BAH=góc DAH
AH chung
Do đó: ΔABH=ΔADH
23 tháng 4 2022
a, Xét Δ ADB và Δ ADE có:
AD chung
góc BAD = góc EAD
AB = AE
⇛Δ ADB =Δ ADE(c-g-c)
DC
2
22 tháng 11 2018
Không spam nha. Chương trình game xin tặng chương trình học online. Nhằm mục đích game được nhiều người chơi.
Thay mặt người đào tạo chương trình hôm nay : Có 200 suất học bỗng cho những học sinh tích cực hoạt động từ bây giờ ( Mỗi suất học bỗng là 100k). Nhận thưởng bằng cách vào google tìm kiếm.
Link như sau vào google hoặc cốc cốc để tìm kiếm:
https://lazi.vn/quiz/d/17912/game-lien-quan-mobile-ra-doi-vao-ngay-thang-nam-nao
Copy cũng được nha
Bạn hack nick mình thu ib dưới vs nha giúp mk chuyện nàynn
22 tháng 11 2018
Kẻ \(AH\perp BC(H\in BC)\)
Có HD và HC lần lượt là hình chiếu của AD,AC trên BC
Mà HD < HC
=> AD < AC \((\)quan hệ đường vuông góc và đường xiên\()\)
Do AB = AD \((gt)\)
=> AB < AC \((đpcm)\)
Chúc bạn học tốt :>
Vẽ hình đi
Ta có HD < HC ( D nằm giữa H và C )
\(\Rightarrow\)AD < AC ( đường xiên và hình chiếu ) ( 1 )
Mà AD = AB ( gt ) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra AB , AC
Vậy AB < AC ( đpcm )