Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3
If mày định trình bày một idea nào đó, mày should dùng brain của mày
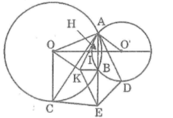
a) Chứng minh ABCD và ADKC là các tứ giác nội tiếp.
b) Từ câu a suy ra \(\widehat{CKB}=\widehat{CDB}\).Ta lại có
\(\widehat{CKE}=\widehat{ECA}=\widehat{CDB}\)
Suy ra\(\widehat{CKB}=\widehat{CKE}\), do đó K, E, B thẳng hàng.